传统遗传算法多使用二进制编码与单点交叉。
但在实际优化问题中,更自然的表示通常是实数编码。
因此,需要一种方法让实数编码的交叉操作仍然具备二进制交叉的特性。
SBX(Simulated Binary Crossover) 由 Deb 和 Agrawal(1995)提出,
其目标是在实数空间中模拟二进制交叉的“统计行为”。
SBX 在每个维度上以两个父代个体 x1 和 x2 为基础(假设 x1≤x2),
生成两个子代 c1 与 c2:
c1c2=0.5[(1+βq)x1+(1−βq)x2],=0.5[(1−βq)x1+(1+βq)x2].
可以验证:
c1+c2=x1+x2,
即 保持父代均值不变(无系统偏移)。
βq 控制子代相对父代的分布范围:
- βq<1:子代在父母之间;
- βq=1:子代正好在中间;
- βq>1:子代超出父代范围(外推)。
βq 的分布决定了交叉算子的搜索行为。
SBX 使用一个分段幂律分布来采样 βq,
由参数 ηc>0(distribution index)控制分布形状。
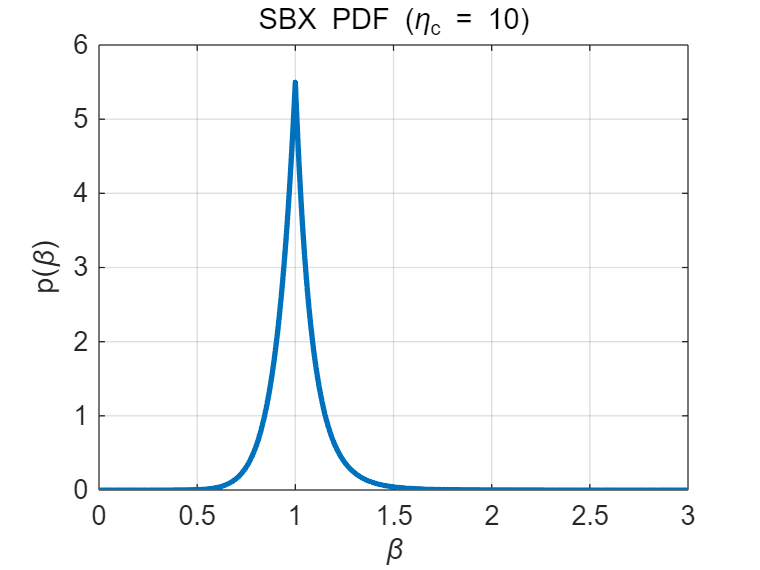
p(β)=⎩⎨⎧21(ηc+1)βηc,21(ηc+1)β−(ηc+2),0≤β≤1,β>1.
F(β)=⎩⎨⎧21βηc+1,1−21β−(ηc+1),0≤β≤1,β>1.
为从该分布中采样,SBX 使用逆变换采样法:
令 u∼U(0,1),则:
β=F−1(u)
当 u≤0.5
u=21βηc+1=>2u=βηc+1=>β=(2u)ηc+11
当 u>0.5
u=1−21β−(ηc+1)=>1−u=21β−(ηc+1)=>2(1−u)=β−(ηc+1)=>2(1−u)1=βηc+1=>β=[2(1−u)1]ηc+11
综上:
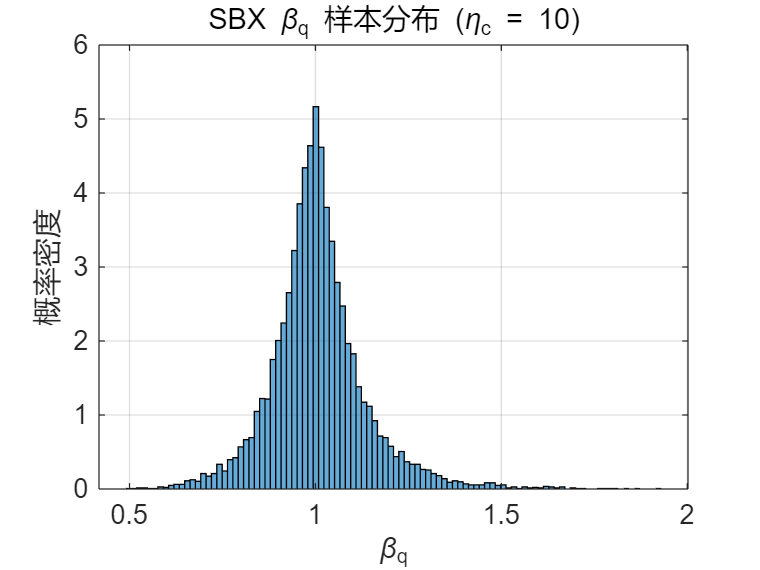
βq=⎩⎨⎧(2u)1/(ηc+1),[2(1−u)1]1/(ηc+1),u≤0.5,u>0.5.
这保证了:
- 一半概率生成 βq≤1(子代在父代区间内);
- 一半概率生成 βq>1(子代在父代区间外)。
| 参数 ηc | 分布特征 | 搜索特性 |
|---|
| 小(2~5) | 分布平坦,尾部长 | 探索性强,外推多 |
| 中(10~20) | 中心集中,尾部适中 | 平衡探索与开发 |
| 大(30~50) | 分布尖锐,接近 β=1 | 开发性强,子代接近父代 |
特点总结:
- 对称性:内外区域各占 50%,模拟二进制交叉的随机性;
- 均值保持:c1+c2=x1+x2;
- 自适应尺度:父代越近,子代变化越小;
- 长尾探索:幂律尾部允许偶尔“跳出”父代范围。
| 算子 | 分布特征 | 外推能力 | 均值保持 | 特点 |
|---|
| 算术交叉 | 固定加权平均 | 无 | 是 | 简单但探索性差 |
| BLX-α | 均匀分布 | 有(α 控制) | 否 | 随机性高但偏移大 |
| SBX | 幂律分布(对称) | 有 | 是 | 兼顾稳定与探索,模拟二进制特性 |
for each dimension j:
if rand() < p_crossover:
u = rand(0,1)
if u <= 0.5:
beta = (2*u)^(1/(ηc+1))
else:
beta = (1/(2*(1-u)))^(1/(ηc+1))
c1[j] = 0.5*((1+beta)*x1[j] + (1-beta)*x2[j])
c2[j] = 0.5*((1-beta)*x1[j] + (1+beta)*x2[j])
else:
c1[j] = x1[j]
c2[j] = x2[j]
# 修正越界:clip 到允许范围
SBX 算子(Simulated Binary Crossover)是实数编码遗传算法中最经典、最常用的交叉算子之一。
它通过一个受控的幂律分布模拟二进制交叉的统计特征,兼顾局部开发与全局探索,并且保持父代均值不偏移。
关键思想:
- 用分布指数 ηc 控制扰动强度;
- 通过逆变换采样精确生成 βq;
- 在实数空间实现二进制交叉的“统计等价性”。

