跳至主要內容

多项式变异

Goat_Yang2025/10/23智能优化算法进化算法算子约 1447 字大约 5 分钟

多项式变异

一、概念与作用

多项式变异（Polynomial Mutation）是一种连续变量的变异算子，广泛应用于进化算法（如 NSGA-II、MOEA/D）中。
其主要思想是：

通过一个可调的多项式分布实现“小扰动概率高，大扰动概率低”的变异机制，
以维持种群多样性并防止早熟收敛。

二、基本形式

设个体的第 ii 个决策变量为 xix_i，定义域为 [xi(L),xi(U)][x_i^{(L)}, x_i^{(U)}]。
变异操作为：

xi′=xi+δi⋅(xi(U)−xi(L))x_i' = x_i + \delta_i \cdot (x_i^{(U)} - x_i^{(L)})

其中 δi\delta_i 是根据多项式分布生成的扰动因子，满足 δi∈[−1,1]\delta_i \in [-1,1]。

三、扰动因子的推导

3.1 设计原则

扰动因子 δ\delta 应满足以下条件：

  1. 对称性：正负方向等概率；
  2. 有界性：δ∈[−1,1]\delta \in [-1,1]；
  3. 可调性：通过参数控制扰动大小分布。

为此，选择如下形式的分布函数：

f(δ)∝(1−∣δ∣)ηm,δ∈[−1,1]f(\delta) \propto (1 - |\delta|)^{\eta_m}, \quad \delta \in [-1,1]

其中 ηm\eta_m 为分布指数（mutation distribution index），
控制分布的尖锐程度。

3.2 概率密度函数（PDF）

归一化条件：

∫−11f(δ) dδ=1\int_{-1}^{1} f(\delta)\, d\delta = 1

由对称性，有：

2∫01C(1−δ)ηmdδ=12 \int_0^1 C (1 - \delta)^{\eta_m} d\delta = 1

解得归一化系数：

C=ηm+12C = \frac{\eta_m + 1}{2}

于是 PDF 为：

p(δ)=ηm+12(1−∣δ∣)ηm,δ∈[−1,1]p(\delta) = \frac{\eta_m + 1}{2} (1 - |\delta|)^{\eta_m}, \quad \delta \in [-1,1]

3.3 累积分布函数（CDF）

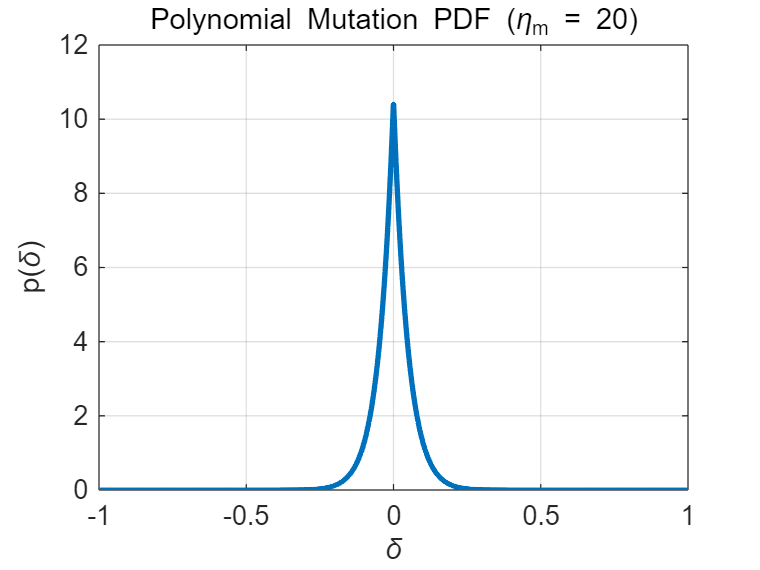
由定义：

F(δ)=∫−1δp(t) dtF(\delta) = \int_{-1}^{\delta} p(t)\,dt

当 δ∈[−1,0]\delta \in [-1, 0]：

F(δ)=12(1+δ)ηm+1F(\delta) = \frac{1}{2}(1 + \delta)^{\eta_m + 1}

当 δ∈[0,1]\delta \in [0, 1]：

F(δ)=1−12(1−δ)ηm+1F(\delta) = 1 - \frac{1}{2}(1 - \delta)^{\eta_m + 1}

由此可得整体的分段形式：

F(δ)={12(1+δ)ηm+1,δ∈[−1,0],1−12(1−δ)ηm+1,δ∈[0,1].F(\delta) = \begin{cases} \frac{1}{2}(1 + \delta)^{\eta_m + 1}, & \delta \in [-1, 0], \\[6pt] 1 - \frac{1}{2}(1 - \delta)^{\eta_m + 1}, & \delta \in [0, 1]. \end{cases}

3.4 逆变换采样（Inverse Transform Sampling）

令 u∼U(0,1)u \sim U(0,1) 为均匀随机数，
根据 u=F(δ)u = F(\delta) 反解得到 δ\delta。

当 u<0.5u < 0.5：

u=12(1+δ)ηm+1⇒δ=(2u)1ηm+1−1u = \frac{1}{2}(1 + \delta)^{\eta_m + 1} \Rightarrow \delta = (2u)^{\frac{1}{\eta_m + 1}} - 1

当 u≥0.5u \ge 0.5：

u=1−12(1−δ)ηm+1⇒δ=1−[2(1−u)]1ηm+1u = 1 - \frac{1}{2}(1 - \delta)^{\eta_m + 1} \Rightarrow \delta = 1 - [2(1 - u)]^{\frac{1}{\eta_m + 1}}

3.5 最终扰动因子定义

δ={(2u)1/(1+ηm)−1,u<0.5,1−[2(1−u)]1/(1+ηm),u≥0.5.\boxed{ \delta = \begin{cases} (2u)^{1/(1+\eta_m)} - 1, & u < 0.5, \\[6pt] 1 - [2(1 - u)]^{1/(1+\eta_m)}, & u \ge 0.5. \end{cases} }

四、边界处理与截断机制

4.1 基本 min–max 截断

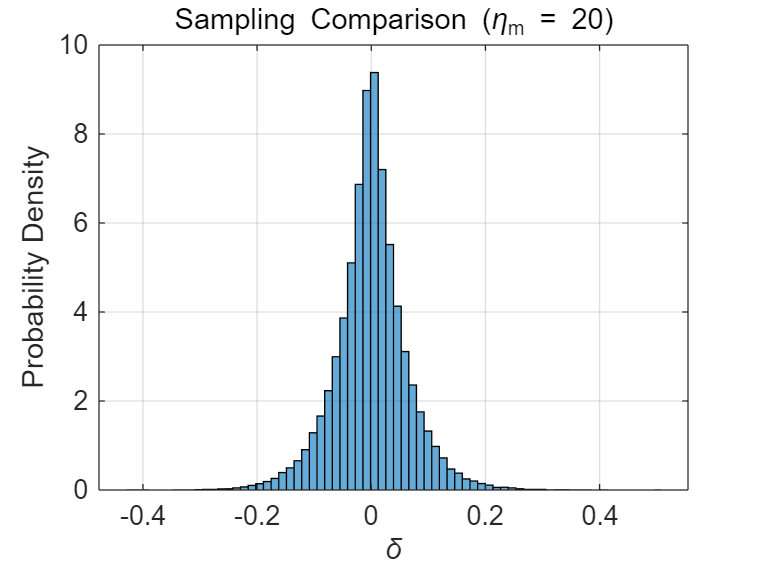
为保证 xi′x_i' 不超出可行域 [xi(L),xi(U)][x_i^{(L)}, x_i^{(U)}]，可采用简单裁剪：

xi′=min⁡(max⁡(xi′,xi(L)),xi(U)).x_i' = \min(\max(x_i', x_i^{(L)}), x_i^{(U)}).

这种方式直接截断越界结果，简单可靠。
但当 xix_i 靠近边界时，可行扰动区间明显不对称，
仍然按原始对称分布采样会造成无效扰动比例高。

4.2 NSGA-II 条件截断采样（精确推导）

为在靠近边界时仍保持正确分布与对称采样概率，
NSGA-II 在每个变量上重新计算可行扰动范围，并对分布进行条件化。

（1）定义可行区间

设：

δ1=xi−xi(L)xi(U)−xi(L),δ2=xi(U)−xixi(U)−xi(L).\delta_1 = \frac{x_i - x_i^{(L)}}{x_i^{(U)} - x_i^{(L)}}, \quad \delta_2 = \frac{x_i^{(U)} - x_i}{x_i^{(U)} - x_i^{(L)}}.

则扰动 δ\delta 的可行范围为：

δ∈[−δ1,δ2].\delta \in [-\delta_1, \delta_2].

（2）截断分布归一化

原始分布 p(δ)∝(1−∣δ∣)ηmp(\delta)\propto(1-|\delta|)^{\eta_m} 被截到 [−δ1,δ2][-\delta_1,\delta_2]。
归一化常数为：

Z=1−12[(1−δ1)ηm+1+(1−δ2)ηm+1].Z = 1 - \frac{1}{2}\Big[(1 - \delta_1)^{\eta_m + 1} + (1 - \delta_2)^{\eta_m + 1}\Big].

左、右两侧概率质量分别为：

pleft=1−(1−δ1)ηm+12Z,pright=1−pleft.p_{\text{left}} = \frac{1 - (1 - \delta_1)^{\eta_m + 1}}{2Z}, \quad p_{\text{right}} = 1 - p_{\text{left}}.

（3）分段逆变换采样

令 u∼U(0,1)u \sim U(0,1)，若 u<pleftu < p_{\text{left}}，则 δ∈[−δ1,0]\delta \in [-\delta_1, 0]；
否则 δ∈[0,δ2]\delta \in [0, \delta_2]。

左侧：

u′=upleft,δ=[(1−δ1)ηm+1+(1−(1−δ1)ηm+1)u′]1ηm+1−1.u' = \frac{u}{p_{\text{left}}}, \quad \delta = \bigl[(1 - \delta_1)^{\eta_m + 1} + \bigl(1 - (1 - \delta_1)^{\eta_m + 1}\bigr)u'\bigr]^{\frac{1}{\eta_m + 1}} - 1.

右侧：

u′=u−pleftpright,δ=1−[(1−δ2)ηm+1+(1−(1−δ2)ηm+1)(1−u′)]1ηm+1.u' = \frac{u - p_{\text{left}}}{p_{\text{right}}}, \quad \delta = 1 - \bigl[(1 - \delta_2)^{\eta_m + 1} + \bigl(1 - (1 - \delta_2)^{\eta_m + 1}\bigr)(1 - u')\bigr]^{\frac{1}{\eta_m + 1}}.

这样可确保：

  • 当 xix_i 靠近边界时，有效扰动自动压缩；
  • 当 xix_i 处于中间区间时，恢复到标准多项式变异分布。

（4）工程化写法（NSGA-II 常见实现）

实际中常用的 NSGA-II 实现，将条件截断的采样写成一个紧凑形式。
设：

mut_pow=1ηm+1,δ1=xi−xi(L)xi(U)−xi(L),δ2=xi(U)−xixi(U)−xi(L).\text{mut\_pow} = \frac{1}{\eta_m + 1}, \quad \delta_1 = \frac{x_i - x_i^{(L)}}{x_i^{(U)} - x_i^{(L)}}, \quad \delta_2 = \frac{x_i^{(U)} - x_i}{x_i^{(U)} - x_i^{(L)}}.

随机生成 u∼U(0,1)u \sim U(0,1)，则扰动 Δq\Delta q 的计算为：

Δq={[ 2u+(1−2u)(1−δ1)ηm+1 ]mut_pow−1,u≤0.5,1−[ 2(1−u)+2(u−0.5)(1−δ2)ηm+1 ]mut_pow,u>0.5.\Delta q = \begin{cases} \left[\,2u + (1 - 2u)(1 - \delta_1)^{\eta_m + 1}\,\right]^{\text{mut\_pow}} - 1, & u \le 0.5, \\[8pt] 1 - \left[\,2(1 - u) + 2(u - 0.5)(1 - \delta_2)^{\eta_m + 1}\,\right]^{\text{mut\_pow}}, & u > 0.5. \end{cases}

最终得到变异后的变量：

xi′=xi+Δq⋅(xi(U)−xi(L)),x_i' = x_i + \Delta q \cdot (x_i^{(U)} - x_i^{(L)}),

并进行边界裁剪（防止舍入误差或极端边界情况）：

xi′=min⁡ ⁣(max⁡(xi′, xi(L)), xi(U)).x_i' = \min\!\bigl(\max(x_i',\, x_i^{(L)}),\, x_i^{(U)}\bigr).

✅ 该形式与严格推导的条件截断采样等价，
其中 δ1\delta_1、δ2\delta_2 自动约束可行变异范围，
从而实现数值稳定、结构简单的多项式变异。

五、参数含义与影响

参数含义典型取值影响
ηm\eta_m变异分布指数10～50控制扰动幅度分布
PmP_m变异概率1/n1/n 或 0.1控制变异频率
δ1,δ2\delta_1, \delta_2相对边界位置(0,1)控制可行变异范围

六、MATLAB 实现示例

function x_new = polynomial_mutation(x, lower, upper, eta_m, p_m)
    n = numel(x);
    x_new = x;
    for i = 1:n
        if rand < p_m
            xl = lower(i); xu = upper(i);
            delta1 = (x(i) - xl) / (xu - xl);
            delta2 = (xu - x(i)) / (xu - xl);
            u = rand; mut_pow = 1 / (eta_m + 1);
            if u <= 0.5
                xy = 1 - delta1;
                val = 2*u + (1 - 2*u)*xy^(eta_m + 1);
                deltaq = val^mut_pow - 1;
            else
                xy = 1 - delta2;
                val = 2*(1 - u) + 2*(u - 0.5)*xy^(eta_m + 1);
                deltaq = 1 - val^mut_pow;
            end
            x_new(i) = x(i) + deltaq * (xu - xl);
            x_new(i) = min(max(x_new(i), xl), xu);
        end
    end
end

七、小结

项目内容
核心思想小变异多，大变异少
扰动控制通过 ηm\eta_m 调整分布陡峭度
生成方式逆变换采样（Inverse Transform Sampling）
边界处理min–max 裁剪（或更高级的条件截断）
常见用途连续变量优化（NSGA-II、MOEA/D 等）
感谢访问
Copyright © 2025 Goat_Yang