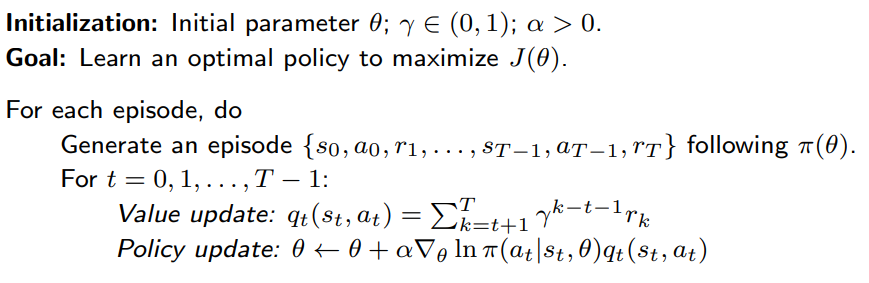在本文中,我们将从
- 基于价值的方法转向基于策略的方法
- 基于价值函数的方法转向策略函数方法(或称为策略梯度方法)
以前,策略是通过表格表示的:
- 所有状态的动作概率存储在表格π(a∣s)中。表格中的每个条目由状态和动作索引。
| a1 | a2 | a3 | a4 | a5 |
|---|
| s1 | $\pi(a_1 | s_1)$ | $\pi(a_2 | s_1)$ | $\pi(a_3 |
| ... | ... | ... | ... | ... | ... |
| s9 | $\pi(a_1 | s_9)$ | $\pi(a_2 | s_9)$ | $\pi(a_3 |
现在,策略可以通过参数化函数表示:
π(a∣s,θ)
其中θ∈Rm是一个参数向量。
- 该函数可以是一个神经网络,其输入为s,输出为采取每个动作的概率,参数为θ。
- 优势:当状态空间较大时,表格表示在存储和泛化效率上较低。
- 函数表示有时也写作π(a,s,θ)、πθ(a∣s)或πθ(a,s)。
首先,如何定义最优策略?
- 在表格表示的情况下,策略π是最优的,如果它能最大化每个状态值。
- 在函数表示的情况下,策略π是最优的,如果它能最大化某些标量指标。
第二,如何访问动作的概率?
- 在表格表示的情况下,采取动作a在状态s时的概率可以直接通过查表获取。
- 在函数表示的情况下,给定函数结构和参数,我们需要计算函数π(a∣s,θ)的值。
第三,如何更新策略?
- 在表格表示的情况下,策略π可以通过直接修改表格中的条目来更新。
- 在函数表示的情况下,策略π不能再以这种方式更新。相反,它只能通过改变参数θ来更新。
- 首先,使用度量(或目标函数)来定义最优策略:J(θ),它可以定义最优策略。
- 其次,使用基于梯度的优化算法来搜索最优策略:
θt+1=θt+α∇θJ(θt)
第一个指标是平均状态价值,或简称平均价值:
vˉπ=s∈S∑d(s)vπ(s)
- vˉπ 是状态价值的加权平均。
- d(s)≥0 是状态 s 的权重。
由于 ∑s∈Sd(s)=1,我们可以将 d(s) 解释为一个概率分布。因此,该指标也可以写作:
vˉπ=ES∼d[vπ(S)]
如何选择 d0?
一种简单方法是认为所有状态同等重要,因此选择:
d0(s)=1/∣S∣
另一种重要情况是我们只关注某个特定状态 s0。例如,在某些任务中,每次训练从同一个状态 s0 开始,此时我们只关注从 s0 开始的长期回报。这种情况下:
d0(s0)=1,d0(s=s0)=0
因此,此时:
vˉπ=vπ(s0)
在文献中你经常会看到以下指标:
J(θ)=n→∞limE[t=0∑nγtRt+1]=E[t=0∑∞γtRt+1]
它们是相同的**,因为:
J(θ)=E[t=0∑∞γtRt+1]=s∈S∑d(s)E[t=0∑∞γtRt+1∣S0=s]=s∈S∑d(s)vπ(s)=vˉπ
第二个指标是平均一步奖励,或简称平均奖励:
rˉπ≐s∈S∑dπ(s)rπ(s)=E[rπ(S)],
其中 S∼dπ,
rπ(s)r(s,a)=a∈A∑π(a∣s)r(s,a)=E[R∣s,a]=r∑rp(r∣s,a)
备注:
- rˉπ 就是即时奖励的加权平均;
- rπ(s) 是从状态 s 可获得的平均即时奖励;
- dπ 是平稳分布。
- 假设一个智能体遵循某个策略并生成一条轨迹,其奖励序列为 (R1,R2,…)。
- 沿该轨迹的平均单步奖励为:
=n→∞limn1E[R1+R2+⋯+Rn∣S0=s0]n→∞limn1E[t=0∑n−1Rt+1∣S0=s0]
其中 s0 是轨迹的起始状态。
一个重要事实是:
n→∞limn1E[t=0∑n−1Rt+1∣S0=s0]=n→∞limn1E[t=0∑n−1Rt+1]=s∑dπ(s)rπ(s)=rˉπ
备注:
- 重点: 起始状态 s0 无关紧要;
- 方程的推导过程并不简单,可在我的书中找到详细解释。
| 指标 (Metric) | 表达式 1 (Expression 1) | 表达式 2 (Expression 2) | 表达式 3 (Expression 3) |
|---|
| vˉπ | ∑s∈Sd(s)vπ(s) | ES∼d[vπ(S)] | limn→∞E[∑t=0nγtRt+1] |
| rˉπ | ∑s∈Sdπ(s)rπ(s) | ES∼dπ[rπ(S)] | limn→∞n1E[∑t=0n−1Rt+1] |
备注 1:
- 所有这些指标都是策略 π 的函数。
- 由于策略 π 是由参数 θ 表示的,因此这些指标也是 θ 的函数。
- 换句话说,不同的 θ 值可以产生不同的指标值。
因此,我们可以搜索使指标最大的最优的 θ 值。 这正是策略梯度方法的基本思想。
备注 2:
- 一个复杂之处在于,这些指标可以在折扣情形(γ∈(0,1))或非折扣情形(γ=1)下定义;
- 非折扣情形并不简单;
- 本文目前只考虑折扣情形。关于非折扣情形的更多内容,请参阅教材。
备注 3:
rˉπ 和 vˉπ 之间是什么关系?
这两个指标是等价的(但不相等)。具体来说,在折扣情形 γ<1 时,有:
rˉπ=(1−γ)vˉπ
因此,它们可以同时最大化。
给定一个指标,接下来我们将:
- 推导它的梯度;
- 然后,应用基于梯度的方法来优化该指标。
梯度的计算是策略梯度方法中最复杂的部分之一!
这是因为:
- 首先,我们需要区分不同的指标:vˉπ,rˉπ,vˉπ0;
- 其次,我们需要区分折扣情况和非折扣情况。
∇θJ(θ)=s∈S∑η(s)a∈A∑∇θπ(a∣s,θ)qπ(s,a)
以上是一个统一形式,适用于多种情况:
- J(θ) 可以是 vˉπ、rˉπ 或 vˉπ0;
- 等号 "=" 可以表示严格等于、近似等于或成比例;
- η 是状态的分布或权重。
相关信息
这个表达式的推导非常复杂,此处不赘述。 对于大多数读者,掌握这个表达式就足够了。
一个简洁且重要的梯度表达式:
∇θJ(θ)=s∈S∑η(s)a∈A∑∇θπ(a∣s,θ)qπ(s,a)=ES∼η,A∼π[∇θlnπ(A∣S,θ)qπ(S,A)]
∇θJ≈∇θlnπ(a∣s,θ)qπ(s,a)
其中 s,a 是采样值。这就是随机梯度下降(SGD)的核心思想。
证明:考虑函数 lnπ,其中 ln 表示自然对数。显然有:
∇θlnπ(a∣s,θ)=π(a∣s,θ)∇θπ(a∣s,θ)
因此,
∇θπ(a∣s,θ)=π(a∣s,θ)∇θlnπ(a∣s,θ)
于是我们有:
∇θJ=s∑η(s)a∑∇θπ(a∣s,θ)qπ(s,a)=s∑η(s)a∑π(a∣s,θ)∇θlnπ(a∣s,θ)qπ(s,a)=ES∼η[a∑π(a∣S,θ)∇θlnπ(a∣S,θ)qπ(S,a)]=ES∼η,A∼π[∇θlnπ(A∣S,θ)qπ(S,A)]
由 lnπ(a∣s,θ) 的定义可知,对于所有的 s,a,θ,我们必须有:
π(a∣s,θ)>0
这可以通过使用Softmax 函数来实现,它能够将任意向量从 (−∞,+∞) 映射到 (0,1):
例如,对于任意向量 x=[x1,…,xn]T:
zi=∑j=1nexjexi
其中 zi∈(0,1) 且 ∑i=1nzi=1。
策略函数具体形式为:
π(a∣s,θ)=∑a′∈Aeh(s,a′,θ)eh(s,a,θ)
其中 h(s,a,θ) 是需要学习的另一个函数。
这种基于 Softmax 的形式可以通过一个神经网络实现,其输入是 s,参数是 θ。网络的输出维度是 ∣A∣,每个输出对应一个动作 a 的 π(a∣s,θ)。输出层的激活函数应为 Softmax。
由于 π(a∣s,θ)>0 对所有动作 a 成立,因此该参数化策略是随机的(stochastic),具有一定的探索性(exploratory)。
- 此外,也存在确定性策略梯度(Deterministic Policy Gradient, DPG)方法。
Gradient-ascent algorithm 梯度上升算法
现在,我们介绍第一个策略梯度算法,用于寻找最优策略!
1)最大化 J(θ) 的梯度上升算法如下:
θt+1=θt+α∇θJ(θt)=θt+αE[∇θlnπ(A∣S,θt)qπ(S,A)]
2)由于真实梯度不可得,我们用随机版本替代:
θt+1=θt+α∇θlnπ(at∣st,θt)qπ(st,at)
3)此外,qπ 不可得,我们再用估计值替代:
θt+1=θt+α∇θlnπ(at∣st,θt)估计值qt(st,at)
- 如果 qπ(st,at) 由蒙特卡洛估计获得,该算法有一个专属名字:REINFORCE
- REINFORCE 是最早且最简单的策略梯度算法之一。
- 很多其他策略梯度方法(如 actor-critic 方法)都可以视作对 REINFORCE 的扩展。
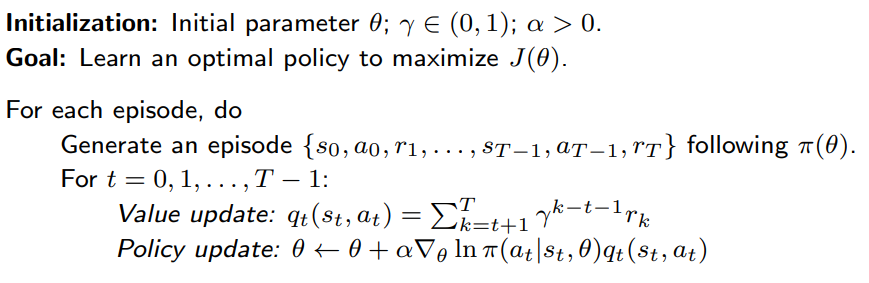
ES∼η,A∼π[∇θlnπ(A∣S,θt)qπ(S,A)]⇒∇θlnπ(a∣s,θt)qπ(s,a)
如何采样 S?
- S∼η,其中 η 是策略 π 下的长期行为分布;
- 实际中人们通常不关心它的具体形式。
如何采样 A?
- A∼π(A∣S,θ),因此 at 应该按照当前策略 π(θt) 在 st 下采样。
- 因此,策略梯度方法是 on-policy 的。
由于:
∇θlnπ(at∣st,θt)=π(at∣st,θt)∇θπ(at∣st,θt)
算法可以重写为:
θt+1=θt+α∇θlnπ(at∣st,θt)qt(st,at)=θt+αβt(π(at∣st,θt)qt(st,at))∇θπ(at∣st,θt)
因此,我们有一个重要的算法表达式:
θt+1=θt+αβt∇θπ(at∣st,θt)
假设 α 足够小。
对上述更新的直觉解释如下:
解释:
若 βt>0,则选择 (st,at) 的概率上升:
π(at∣st,θt+1)>π(at∣st,θt)
若 βt<0,则选择 (st,at) 的概率下降:
π(at∣st,θt+1)<π(at∣st,θt)
数学推导:
当 θt+1−θt 足够小时,由微分定义有:
π(at∣st,θt+1)≈π(at∣st,θt)+(∇θπ(at∣st,θt))T(θt+1−θt)=π(at∣st,θt)+αβt(∇θπ(at∣st,θt))T(∇θπ(at∣st,θt))=π(at∣st,θt)+αβt∥∇θπ(at∣st,θt)∥2
原因如下:
首先,βt 与 qt(st,at) 成正比:
值越大 qt(st,at)⇒值越大 βt⇒值越大 π(at∣st,θt+1)
因此,算法**倾向于利用(exploit)**高价值的动作。
其次,βt 与 π(at∣st,θt) 成反比(当 qt(st,at)>0):
值越小 π(at∣st,θt)⇒值越大 βt⇒值越大 π(at∣st,θt+1)
因此,算法**倾向于探索(explore)**那些原本概率较低的动作。