随机近似算法（Stochastic Approximation, SA）

• 随机逼近（SA）是指一大类随机迭代算法，用于求解求根问题或优化问题。

• 与许多其他求根算法（例如基于梯度的方法）相比，

  SA 的强大之处在于：它不需要知道目标函数的具体表达式，也不需要其导数。

算法示例：期望值估计

▷ 如何计算均值 $\bar{x}$？

$$\mathbb{E}[X] \approx \bar{x} := \frac{1}{N} \sum_{i=1}^{N} x_i .$$

我们有两种方法。

• 第一种方法是最直接的：先收集所有样本，然后再计算平均值。

  • 这种方法的缺点在于：如果样本是随着时间逐个收集的，那么我们必须等待所有样本都收集完成之后，才能计算均值。

• 第二种方法可以避免上述缺点，因为它以一种增量式（incremental）、**迭代式（iterative）**的方式来计算平均值。

​ 特别地，假设

$$w_{k+1} = \frac{1}{k} \sum_{i=1}^{k} x_i, \qquad k = 1, 2, \ldots$$

​ 因此，

$$w_k = \frac{1}{k-1} \sum_{i=1}^{k-1} x_i, \qquad k = 2, 3, \ldots$$

​ 那么，$w_{k+1}$ 可以用 $w_k$ 表示为

$$\begin{aligned} w_{k+1} &= \frac{1}{k} \sum_{i=1}^{k} x_i \\ &= \frac{1}{k} \left( \sum_{i=1}^{k-1} x_i + x_k \right) \\ &= \frac{1}{k} \left( (k-1) w_k + x_k \right) \\ &= w_k - \frac{1}{k} (w_k - x_k). \end{aligned}$$

​ 因此，我们得到如下迭代算法：

$$w_{k+1} = w_k - \frac{1}{k} (w_k - x_k).$$

• 该算法的一个优点在于它是**增量式（incremental）**的。

  一旦接收到一个样本，就可以立即得到均值的估计，并且该均值估计可以立刻用于其他目的。

• 由于在初始阶段样本数量不足，均值估计在一开始并不精确（即 $w_k \neq \mathbb{E}[X]$）。

  然而，这种估计总比没有要好。随着样本数量的不断增加，估计值可以被逐步改进，也就是说，当 $k \to \infty$ 时，

  $$w_k \to \mathbb{E}[X].$$

此外，考虑一种具有更一般形式的算法：

$$w_{k+1} = w_k - \alpha_k (w_k - x_k),$$

其中，用 $\alpha_k > 0$ 替代了 $\frac{1}{k}$。

• 该算法是否仍然收敛到均值 $\mathbb{E}[X]$？

  我们将证明：如果 $\{\alpha_k\}$ 满足一些较弱的条件，那么答案是肯定的。

• 我们还将说明，该算法是一个特殊的随机逼近（stochastic approximation, SA）算法，同时也是一个特殊的随机梯度下降（stochastic gradient descent）算法。

• 在下一讲中，我们将看到时序差分（temporal-difference, TD）算法具有类似但更为复杂的表达形式。

---

Robbins-Monro（RM）算法

• 这是随机逼近领域中的一项开创性（pioneering）工作。

• 著名的随机梯度下降（stochastic gradient descent, SGD）算法是 RM 算法的一种特殊形式。

• RM 算法还可以用于分析前面介绍的均值估计算法。

问题描述（Problem statement）

假设我们希望求解如下方程的根：

$$g(w) = 0,$$

其中，$w \in \mathbb{R}$ 是需要求解的变量，$g : \mathbb{R} \to \mathbb{R}$ 是一个函数。

• 许多问题最终都可以被转化为这样的求根问题。
  例如，假设 $J(w)$ 是一个需要被最小化的目标函数，那么该优化问题可以等价地转化为

  $$g(w) = \nabla_w J(w) = 0.$$

• 需要注意的是，形如 $g(w) = c$（其中 $c$ 为常数）的方程，也可以通过将 $g(w) - c$ 视为一个新的函数，从而转化为上述形式的方程。

求解问题

• 基于模型的方法（Model-based）：

  如果函数 $g$ 的表达式是已知的，那么可以使用许多数值算法来求解该问题。

• 无模型的方法（Model-free）：

  如果函数 $g$ 的表达式是未知的，该怎么办？

  例如，函数可能由一个人工神经网络来表示。

能够求解上述问题的 Robbins–Monro（RM）算法如下所示：

$$w_{k+1} = w_k - a_k \,\tilde{g}(w_k, \eta_k), \qquad k = 1, 2, 3, \ldots$$

其中：

• $w_k$ 是第 $k$ 次对方程根的估计值。

• $\tilde{g}(w_k, \eta_k) = g(w_k) + \eta_k$ 是第 $k$ 次的带噪观测。

  • 为什么这里会有噪声？
    例如，可以将其理解为：对随机变量 $X$ 进行一次随机采样 $x$ 所带来的随机性。

• $a_k$ 是一个正的系数（步长）。

该算法依赖于数据而非模型：

• 输入序列（Input sequence）： $\{ w_k \}$

• 输出序列（含噪声）（Output sequence, noisy）：
  $\{ \tilde{g}(w_k, \eta_k) \}$

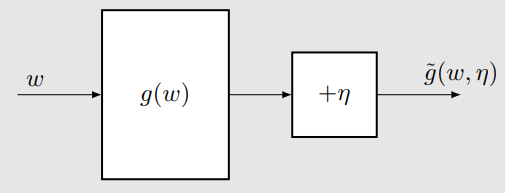
核心思想（Philosophy）：没有模型，就需要数据！

• 函数 $g(w)$ 被视为一个黑箱（black box）。

• 这里所说的“模型”，指的是函数的解析表达式。

收敛性质

直观示例

• 设

  $$g(w) = \tanh(w - 1).$$

• 方程 $g(w) = 0$ 的真实根为

  $$w^* = 1.$$

• 参数设定：

  $$w_1 = 3, \qquad a_k = \frac{1}{k}, \qquad \eta_k \equiv 0$$

  相关信息

  为简化起见，此处不考虑噪声

在这种情况下，Robbins–Monro（RM）算法为

$$w_{k+1} = w_k - a_k\, g(w_k),$$

因为当 $\eta_k = 0$ 时，有 $\tilde{g}(w_k, \eta_k) = g(w_k)$。

仿真结果（Simulation result）

$w_k$ 收敛到真实根 $w^* = 1$。

直觉解释（Intuition）

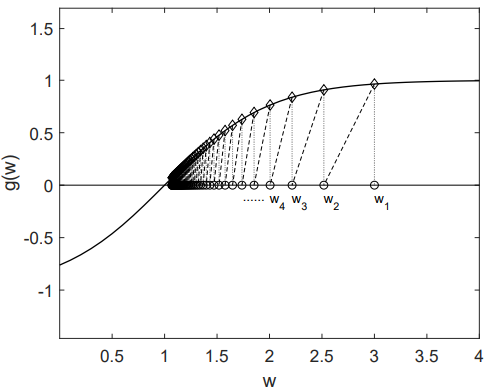
$w_{k+1}$ 比 $w_k$ 更接近 $w^*$。

• 当 $w_k > w^*$ 时，有 $g(w_k) > 0$。此时 $w_{k+1} = w_k - a_k g(w_k) < w_k,$ 因而 $w_{k+1}$ 比 $w_k$ 更接近 $w^*$。

• 当 $w_k < w^*$ 时，有 $g(w_k) < 0$。此时 $w_{k+1} = w_k - a_k g(w_k) > w_k,$ 因而 $w_{k+1}$ 比 $w_k$ 更接近 $w^*$。

上述分析是直观的，但并不严格。下面给出一个严格的收敛性结果。

Robbins–Monro 定理

在 Robbins–Monro 算法中，若满足以下条件：

1. 对所有 $w$，有

   $$0 < c_1 \le \nabla_w g(w) \le c_2 ;$$

2. 步长序列 $\{a_k\}$ 满足

   $$\sum_{k=1}^{\infty} a_k = \infty, \qquad \sum_{k=1}^{\infty} a_k^2 < \infty ;$$

3. 噪声序列 $\{\eta_k\}$ 满足

   $$\mathbb{E}[\eta_k \mid \mathcal{H}_k] = 0, \qquad \mathbb{E}[\eta_k^2 \mid \mathcal{H}_k] < \infty ;$$

其中 $\mathcal{H}_k = \{ w_k, w_{k-1}, \ldots \},$ 则序列 $\{w_k\}$ 以概率 1（w.p.1） 收敛到满足 $g(w^*) = 0$ 的根 $w^*$。

三个条件的解释

• 条件 1： 对所有 $w$，有

  $$0 < c_1 \le \nabla_w g(w) \le c_2$$

  • 函数 $g$ 应当是单调递增的（monotonically increasing），这保证了方程 $g(w) = 0$ 的根存在且唯一。

  • 梯度在上方是有界的。

  • 该条件并不是非常严格。

    例如，考虑 $g(w) = \nabla_w J(w)$ 的情形，此时该条件等价于要求 $g(w)$（或 $J(w)$）是凸的（convex）。

• 条件 2：

  $$\sum_{k=1}^{\infty} a_k = \infty, \qquad \sum_{k=1}^{\infty} a_k^2 < \infty$$

  • $\sum_{k=1}^{\infty} a_k^2 < \infty$ 保证了当 $k \to \infty$ 时，$a_k \to 0$。
  • $\sum_{k=1}^{\infty} a_k = \infty$ 保证了 $a_k$ 不会过快地收敛到 0。

• 条件 3：

  $$\mathbb{E}[\eta_k \mid \mathcal{H}_k] = 0, \qquad \mathbb{E}[\eta_k^2 \mid \mathcal{H}_k] < \infty$$

  相关信息

  相当于均值为0，方差有界

  • 一个特殊但常见的情形是：$\{\eta_k\}$ 是一个 iid 随机序列，满足

    $$\mathbb{E}[\eta_k] = 0, \qquad \mathbb{E}[\eta_k^2] < \infty .$$

  • 观测误差 $\eta_k$ 不要求服从高斯分布。

更深入地考察条件 2

首先，$\sum_{k=1}^{\infty} a_k^2 < \infty$ 表明当 $k \to \infty$ 时，$a_k \to 0$。

• 为什么这个条件重要？

  因为

  $$w_{k+1} - w_k = - a_k \tilde{g}(w_k, \eta_k).$$

  • 若 $a_k \to 0$，则 $a_k \tilde{g}(w_k, \eta_k) \to 0$，从而

    $$w_{k+1} - w_k \to 0.$$

  • 如果 $w_k$ 最终收敛，我们就需要 $w_{k+1} - w_k \to 0$ 这一事实成立。

  • 当 $w_k \to w^*$ 时，有 $g(w_k) \to 0$，此时 $\tilde{g}(w_k, \eta_k)$ 将主要由噪声 $\eta_k$ 所主导。

其次，$\sum_{k=1}^{\infty} a_k = \infty$ 表明 $a_k$ 不能过快地收敛到 0。

• 为什么这个条件重要？

  将

  $$w_2 = w_1 - a_1 \tilde{g}(w_1, \eta_1), \quad w_3 = w_2 - a_2 \tilde{g}(w_2, \eta_2), \ \ldots,$$

  以及

  $$w_{k+1} = w_k - a_k \tilde{g}(w_k, \eta_k)$$

  累加起来，可以得到

  $$w_1 - w_\infty = \sum_{k=1}^{\infty} a_k \tilde{g}(w_k, \eta_k).$$

  假设 $w_\infty = w^*$。如果

  $$\sum_{k=1}^{\infty} a_k < \infty,$$

  那么 $\sum_{k=1}^{\infty} a_k \tilde{g}(w_k, \eta_k)$ 可能是有界的。
  此时，如果初始值 $w_1$ 被选取得距离 $w^*$ 很远，则上述等式将无法成立。

哪些 $\{a_k\}$ 同时满足这两个条件？

一种典型的选择是

$$a_k = \frac{1}{k}.$$

• 有如下结论成立：

  $$\lim_{n \to \infty} \left( \sum_{k=1}^{n} \frac{1}{k} - \ln n \right) = \kappa,$$

  其中 $\kappa \approx 0.577$ 被称为 Euler–Mascheroni 常数（也称为 Euler 常数）。

• 还值得注意的是：

  $$\sum_{k=1}^{\infty} \frac{1}{k^2} = \frac{\pi^2}{6} < \infty.$$

  级数 $\sum_{k=1}^{\infty} \frac{1}{k^2}$ 在数论中有一个专门的名字，称为 巴塞尔问题（Basel problem）。

在实际中，通常选择一个小的正数。此时$\sum_{k=1}^{\infty} a_k = \infty$ 仍然成立，但$\sum_{k=1}^{\infty} a_k^2 < \infty$ 不再成立。选择这个的原因是它能很好地利用后面（k比较大时）得到的样本。实际上算法仍然在某种意义上收敛，可以应对时变系统。

RM算法在期望值估计中的应用

1）考虑如下函数：

$$g(w) \triangleq w - \mathbb{E}[X].$$

我们的目标是求解 $g(w) = 0$。如果能够做到这一点，那么就可以得到 $\mathbb{E}[X]$。

• 均值估计（即求 $\mathbb{E}[X]$）可以被表述为一个求根问题（即求解 $g(w) = 0$）。

2）我们能够获得的观测为

$$\tilde{g}(w, x) \triangleq w - x,$$

因为我们只能获得随机变量 $X$ 的样本。注意到

$$\begin{aligned} \tilde{g}(w, \eta) &= w - x \\ &= w - x + \mathbb{E}[X] - \mathbb{E}[X] \\ &= (w - \mathbb{E}[X]) + (\mathbb{E}[X] - x) \\ &= g(w) + \eta, \end{aligned}$$

其中噪声项 $\eta = \mathbb{E}[X] - x$。

3）用于求解 $g(w) = 0$ 的 RM 算法为

$$w_{k+1} = w_k - \alpha_k \tilde{g}(w_k, \eta_k) = w_k - \alpha_k (w_k - x_k),$$

这恰好就是均值估计算法本身。因此，其收敛性也就自然得到了保证。

---

Dvoretsky 定理

考虑如下随机过程：

$$w_{k+1} = (1 - \alpha_k)\, w_k + \beta_k \eta_k,$$

其中 $\{\alpha_k\}_{k=1}^{\infty}$、$\{\beta_k\}_{k=1}^{\infty}$、$\{\eta_k\}_{k=1}^{\infty}$ 为随机序列，并且对所有 $k$ 有 $\alpha_k \ge 0$、$\beta_k \ge 0$。

若满足以下条件，则 $w_k$ 以概率 1（w.p.1）收敛到 0：

1. $$\sum_{k=1}^{\infty} \alpha_k = \infty, \qquad \sum_{k=1}^{\infty} \alpha_k^2 < \infty, \qquad \sum_{k=1}^{\infty} \beta_k^2 < \infty \quad \text{（以概率 1 一致成立）};$$

2. $$\mathbb{E}[\eta_k \mid \mathcal{H}_k] = 0, \qquad \mathbb{E}[\eta_k^2 \mid \mathcal{H}_k] \le C \quad \text{（以概率 1）},$$

其中

$$\mathcal{H}_k = \{ w_k, w_{k-1}, \ldots, \eta_{k-1}, \ldots, \alpha_{k-1}, \ldots, \beta_{k-1}, \ldots \}.$$

• 该结果比 Robbins–Monro（RM）定理更一般。
  • 它可以用于证明 RM 定理；
  • 它可以用于分析均值估计问题；
  • 其推广形式还可用于分析 Q-learning 与 TD 学习算法。

---

随机梯度下降（Stochastic gradient descent, SGD）

• SGD 在机器学习领域以及强化学习（RL）中被广泛使用。
  • SGD 是一种特殊的 Robbins–Monro（RM）算法。
  • 均值估计算法是 SGD 的一个特殊情形。

问题设定（Problem setup）

假设我们希望求解如下优化问题：

$$\min_{w} \; J(w) = \mathbb{E}[f(w, X)] .$$

• $w$ 是需要被优化的参数。
• $X$ 是一个随机变量，期望是对 $X$ 取的。
• $w$ 和 $X$ 都可以是标量或向量，而函数 $f(\cdot)$ 是一个标量函数。

求解问题

方法 1：梯度下降（Gradient Descent, GD）

$$w_{k+1} = w_k - \alpha_k \nabla_w \mathbb{E}[f(w_k, X)] = w_k - \alpha_k \mathbb{E}[\nabla_w f(w_k, X)] .$$

缺点： 计算期望需要知道随机变量 $X$ 的分布。

相关信息

要模型

方法 2：批量梯度下降（Batch Gradient Descent, BGD）

$$\mathbb{E}[\nabla_w f(w_k, X)] \approx \frac{1}{n} \sum_{i=1}^{n} \nabla_w f(w_k, x_i) .$$

因此，

$$w_{k+1} = w_k - \alpha_k \frac{1}{n} \sum_{i=1}^{n} \nabla_w f(w_k, x_i) .$$

缺点： 对于每一次迭代、每一个 $w_k$，都需要使用大量样本。

方法 3：随机梯度下降（Stochastic Gradient Descent, SGD）

$$w_{k+1} = w_k - \alpha_k \nabla_w f(w_k, x_k) .$$

• 与梯度下降（GD）相比：

  • 用随机梯度 $\nabla_w f(w_k, x_k)$ 替代真实梯度 $\mathbb{E}[\nabla_w f(w_k, X)]$。

• 与批量梯度下降（BGD）相比：

  • 令批量大小 $n = 1$。

SGD的收敛性

SGD 的思想（Idea of SGD）：用随机梯度 $\nabla_w f(w_k, x_k)$替代了真实梯度 $\mathbb{E}[\nabla_w f(w_k, X)]$。

由于

$$\nabla_w f(w_k, x_k) \neq \mathbb{E}[\nabla_w f(w, X)],$$

那么，使用 SGD 时，当 $k \to \infty$，是否有 $w_k \to w^*$？

观察

随机梯度是真实梯度的一个带噪观测：

$$\nabla_w f(w_k, x_k) = \mathbb{E}[\nabla_w f(w, X)] + \bigl( \nabla_w f(w_k, x_k) - \mathbb{E}[\nabla_w f(w, X)] \bigr),$$

其中括号中的部分记为噪声 $\eta$。

SGD 是一种特殊的 Robbins–Monro（RM）算法**，因此其收敛性可以自然推出。

SGD 的收敛性定理

在 SGD 算法中，若满足：

1. 对所有 $w$，$0 < c_1 \le \nabla_w^2 f(w, X) \le c_2 ;$

2. $\sum_{k=1}^{\infty} a_k = \infty, \, \sum_{k=1}^{\infty} a_k^2 < \infty ;$

3. 样本序列 $\{x_k\}_{k=1}^{\infty}$ 是 iid；

则$w_k$以概率 1 收敛到 $\nabla_w \mathbb{E}[f(w, X)] = 0$的解。

证明略

BGD, MBGD, 与SGD

假设我们希望在给定随机样本集合
$\{x_i\}_{i=1}^n$
的情况下，最小化 $J(w) = \mathbb{E}[f(w, X)].$

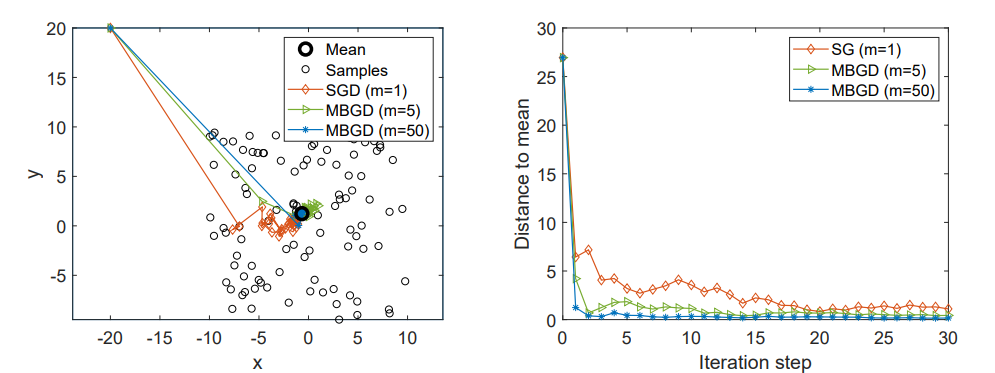
分别用于求解该问题的 BGD、SGD 与 MBGD 算法如下：

批量梯度下降（Batch Gradient Descent, BGD）：

$$w_{k+1} = w_k - \alpha_k \frac{1}{n} \sum_{i=1}^{n} \nabla_w f(w_k, x_i), \qquad (\text{BGD})$$

小批量梯度下降（Mini-batch Gradient Descent, MBGD）：

$$w_{k+1} = w_k - \alpha_k \frac{1}{m} \sum_{j \in \mathcal{I}_k} \nabla_w f(w_k, x_j), \qquad (\text{MBGD})$$

随机梯度下降（Stochastic Gradient Descent, SGD）：

$$w_{k+1} = w_k - \alpha_k \nabla_w f(w_k, x_k), \qquad (\text{SGD})$$

• 在 BGD 算法中，每一次迭代都会使用全部样本。当 $n$ 较大时，$\frac{1}{n} \sum_{i=1}^{n} \nabla_w f(w_k, x_i)$会非常接近真实梯度 $\mathbb{E}[\nabla_w f(w_k, X)].$

• 在 MBGD 算法中，$\mathcal{I}_k$ 是集合 $\{1, \ldots, n\}$ 的一个子集，其大小为 $|\mathcal{I}_k| = m.$集合 $\mathcal{I}_k$ 由 $m$ 次独立同分布（iid）采样得到。

• 在 SGD 算法中，在第 $k$ 次迭代时，$x_k$是从样本集合 $\{x_i\}_{i=1}^n$ 中随机抽取的一个样本。