对于单过程:
S t → A t R t + 1 , S t + 1 S_t \xrightarrow{A_t} R_{t+1},\, S_{t+1} S t A t R t + 1 , S t + 1
S t S_t S t A t A_t A t R t + 1 R_{t+1} R t + 1
均为随机变量
S t → A t S_t \rightarrow A_t S t → A t π ( A t = a ∣ S t = s ) \pi(A_t = a \mid S_t = s) π ( A t = a ∣ S t = s )
S t , A t → R t + 1 S_t, A_t \rightarrow R_{t+1} S t , A t → R t + 1 p ( R t + 1 = r ∣ S t = s , A t = a ) p(R_{t+1} = r \mid S_t = s, A_t = a) p ( R t + 1 = r ∣ S t = s , A t = a )
S t , A t → S t + 1 S_t, A_t \rightarrow S_{t+1} S t , A t → S t + 1 p ( S t + 1 = s ′ ∣ S t = s , A t = a ) p(S_{t+1} = s' \mid S_t = s, A_t = a) p ( S t + 1 = s ′ ∣ S t = s , A t = a )
对于多过程:
S t → A t R t + 1 , S t + 1 → A t + 1 R t + 2 , S t + 2 → A t + 2 R t + 3 , … S_t \xrightarrow{A_t} R_{t+1},\, S_{t+1} \xrightarrow{A_{t+1}} R_{t+2},\, S_{t+2} \xrightarrow{A_{t+2}} R_{t+3},\, \ldots S t A t R t + 1 , S t + 1 A t + 1 R t + 2 , S t + 2 A t + 2 R t + 3 , …
discounted return = G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ \text{discounted return}=G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots discounted return = G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯
The expectation of G t G_t G t
v π ( s ) = E [ G t ∣ S t = s ] v_\pi(s) = \mathbb{E}\!\left[ G_t \mid S_t = s \right] v π ( s ) = E [ G t ∣ S t = s ]
是 s 的函数,从 s 开始的状态价值
基于策略 π \pi π
是多个Trajectory的return的均值
1.提取 G t G_t G t γ \gamma γ
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ = R t + 1 + γ ( R t + 2 + γ R t + 3 + ⋯ ) = R t + 1 + γ G t + 1 . \begin{aligned} G_t &= R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots \\ &= R_{t+1} + \gamma \left( R_{t+2} + \gamma R_{t+3} + \cdots \right) \\ &= R_{t+1} + \gamma G_{t+1}. \end{aligned} G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ = R t + 1 + γ ( R t + 2 + γ R t + 3 + ⋯ ) = R t + 1 + γ G t + 1 .
2. 应用到状态价值公式
v π ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ] . \begin{aligned} v_\pi(s) &= \mathbb{E}\!\left[ G_t \mid S_t = s \right] \\ &= \mathbb{E}\!\left[ R_{t+1} + \gamma G_{t+1} \mid S_t = s \right] \\ &= \mathbb{E}\!\left[ R_{t+1} \mid S_t = s \right] + \gamma \mathbb{E}\!\left[ G_{t+1} \mid S_t = s \right]. \end{aligned} v π ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ] .
对于第一部分 E [ R t + 1 ∣ S t = s ] \mathbb{E}\!\left[ R_{t+1} \mid S_t = s \right] E [ R t + 1 ∣ S t = s ]
E [ R t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) E [ R t + 1 ∣ S t = s , A t = a ] = ∑ a π ( a ∣ s ) ∑ r p ( r ∣ s , a ) r . \begin{aligned} \mathbb{E}\!\left[ R_{t+1} \mid S_t = s \right] &= \sum_a \pi(a \mid s)\, \mathbb{E}\!\left[ R_{t+1} \mid S_t = s, A_t = a \right] \\ &= \sum_a \pi(a \mid s)\, \sum_r p(r \mid s, a)\, r . \end{aligned} E [ R t + 1 ∣ S t = s ] = a ∑ π ( a ∣ s ) E [ R t + 1 ∣ S t = s , A t = a ] = a ∑ π ( a ∣ s ) r ∑ p ( r ∣ s , a ) r .
对于第二部分 E [ G t + 1 ∣ S t = s ] \mathbb{E}\!\left[ G_{t+1} \mid S_t = s \right] E [ G t + 1 ∣ S t = s ]
E [ G t + 1 ∣ S t = s ] = ∑ s ′ E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] p ( s ′ ∣ s ) = ∑ s ′ E [ G t + 1 ∣ S t + 1 = s ′ ] p ( s ′ ∣ s ) = ∑ s ′ v π ( s ′ ) p ( s ′ ∣ s ) = ∑ s ′ v π ( s ′ ) ∑ a p ( s ′ ∣ s , a ) π ( a ∣ s ) . \begin{aligned} \mathbb{E}\!\left[ G_{t+1} \mid S_t = s \right] &= \sum_{s'} \mathbb{E}\!\left[ G_{t+1} \mid S_t = s, S_{t+1} = s' \right] p(s' \mid s) \\ &= \sum_{s'} \mathbb{E}\!\left[ G_{t+1} \mid S_{t+1} = s' \right] p(s' \mid s) \\ &= \sum_{s'} v_\pi(s')\, p(s' \mid s) \\ &= \sum_{s'} v_\pi(s') \sum_a p(s' \mid s, a)\, \pi(a \mid s). \end{aligned} E [ G t + 1 ∣ S t = s ] = s ′ ∑ E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] p ( s ′ ∣ s ) = s ′ ∑ E [ G t + 1 ∣ S t + 1 = s ′ ] p ( s ′ ∣ s ) = s ′ ∑ v π ( s ′ ) p ( s ′ ∣ s ) = s ′ ∑ v π ( s ′ ) a ∑ p ( s ′ ∣ s , a ) π ( a ∣ s ) .
相关信息
E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] = E [ G t + 1 ∣ S t + 1 = s ′ ] \mathbb{E}\left[ G_{t+1} \mid S_t = s, S_{t+1} = s' \right] = \mathbb{E}\left[ G_{t+1} \mid S_{t+1} = s'\right] E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] = E [ G t + 1 ∣ S t + 1 = s ′ ]
v π ( s ) = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) ∑ r p ( r ∣ s , a ) r ⏟ mean of immediate rewards + γ ∑ a π ( a ∣ s ) ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) ⏟ mean of future rewards = ∑ a π ( a ∣ s ) [ ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) ] , ∀ s ∈ S . \begin{aligned} v_\pi(s) &= \mathbb{E}\!\left[ R_{t+1} \mid S_t = s \right] + \gamma \, \mathbb{E}\!\left[ G_{t+1} \mid S_t = s \right] \\[6pt] &= \underbrace{\sum_a \pi(a \mid s) \sum_r p(r \mid s, a)\, r}_{\text{mean of immediate rewards}} + \gamma \, \underbrace{\sum_a \pi(a \mid s) \sum_{s'} p(s' \mid s, a)\, v_\pi(s')}_{\text{mean of future rewards}} \\[6pt] &= \sum_a \pi(a \mid s) \left[ \sum_r p(r \mid s, a)\, r + \gamma \sum_{s'} p(s' \mid s, a)\, v_\pi(s') \right], \qquad \forall s \in \mathcal{S}. \end{aligned} v π ( s ) = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ] = mean of immediate rewards a ∑ π ( a ∣ s ) r ∑ p ( r ∣ s , a ) r + γ mean of future rewards a ∑ π ( a ∣ s ) s ′ ∑ p ( s ′ ∣ s , a ) v π ( s ′ ) = a ∑ π ( a ∣ s ) [ r ∑ p ( r ∣ s , a ) r + γ s ′ ∑ p ( s ′ ∣ s , a ) v π ( s ′ ) ] , ∀ s ∈ S .
贝尔曼公式是不同状态的状态价值的关系的函数 是公式集合,每个状态都有想这样的公式 公式变量含义
v π ( s ) v_\pi(s) v π ( s ) v π ( s ′ ) v_\pi(s') v π ( s ′ )
π ( a ∣ s ) \pi(a \mid s) π ( a ∣ s )
p ( r ∣ s , a ) p(r \mid s, a) p ( r ∣ s , a ) p ( s ′ ∣ s , a ) p(s' \mid s, a) p ( s ′ ∣ s , a )
对于状态集合的每个状态都有一个贝尔曼公式,共 ∣ S ∣ |\mathcal{S}| ∣ S ∣
将贝尔曼方程改写为:
v π ( s ) = r π ( s ) + γ ∑ s ′ p π ( s ′ ∣ s ) v π ( s ′ ) (1) v_{\pi}(s)=r_{\pi}(s)+\gamma\sum_{s'}p_{\pi}(s'\mid s)\,v_{\pi}(s') \tag{1} v π ( s ) = r π ( s ) + γ s ′ ∑ p π ( s ′ ∣ s ) v π ( s ′ ) ( 1 )
其中,
r π ( s ) : = ∑ a π ( a ∣ s ) ∑ r p ( r ∣ s , a ) r , p π ( s ′ ∣ s ) : = ∑ a π ( a ∣ s ) p ( s ′ ∣ s , a ) . r_{\pi}(s):=\sum_{a}\pi(a\mid s)\sum_{r}p(r\mid s,a)\,r,\qquad p_{\pi}(s'\mid s):=\sum_{a}\pi(a\mid s)\,p(s'\mid s,a). r π ( s ) := a ∑ π ( a ∣ s ) r ∑ p ( r ∣ s , a ) r , p π ( s ′ ∣ s ) := a ∑ π ( a ∣ s ) p ( s ′ ∣ s , a ) .
假设状态可以编号为 s i ( i = 1 , … , n ) s_i\ (i=1,\ldots,n) s i ( i = 1 , … , n )
对于状态 s i s_i s i
v π ( s i ) = r π ( s i ) + γ ∑ s j p π ( s j ∣ s i ) v π ( s j ) . v_{\pi}(s_i)=r_{\pi}(s_i)+\gamma\sum_{s_j}p_{\pi}(s_j\mid s_i)\,v_{\pi}(s_j). v π ( s i ) = r π ( s i ) + γ s j ∑ p π ( s j ∣ s i ) v π ( s j ) .
将所有状态对应的方程合在一起,并改写为矩阵-向量形式:
v π = r π + γ P π v π . \mathbf{v}_{\pi}=\mathbf{r}_{\pi}+\gamma \mathbf{P}_{\pi}\mathbf{v}_{\pi}. v π = r π + γ P π v π .
其中
v π : = [ v π ( s 1 ) , … , v π ( s n ) ] T ∈ R n \mathbf{v}_{\pi}:=\bigl[v_{\pi}(s_1),\ldots,v_{\pi}(s_n)\bigr]^{\mathsf T}\in\mathbb{R}^n v π := [ v π ( s 1 ) , … , v π ( s n ) ] T ∈ R n
r π : = [ r π ( s 1 ) , … , r π ( s n ) ] T ∈ R n \mathbf{r}_{\pi}:=\bigl[r_{\pi}(s_1),\ldots,r_{\pi}(s_n)\bigr]^{\mathsf T}\in\mathbb{R}^n r π := [ r π ( s 1 ) , … , r π ( s n ) ] T ∈ R n
P π ∈ R n × n \mathbf{P}_{\pi}\in\mathbb{R}^{n\times n} P π ∈ R n × n [ P π ] i j : = p π ( s j ∣ s i ) [\mathbf{P}{\pi}]{ij}:=p_{\pi}(s_j\mid s_i) [ P π ] ij := p π ( s j ∣ s i )
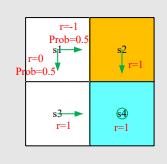
如果有四个状态
[ v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) ] ⏟ v π = [ r π ( s 1 ) r π ( s 2 ) r π ( s 3 ) r π ( s 4 ) ] ⏟ r π + γ [ p π ( s 1 ∣ s 1 ) p π ( s 2 ∣ s 1 ) p π ( s 3 ∣ s 1 ) p π ( s 4 ∣ s 1 ) p π ( s 1 ∣ s 2 ) p π ( s 2 ∣ s 2 ) p π ( s 3 ∣ s 2 ) p π ( s 4 ∣ s 2 ) p π ( s 1 ∣ s 3 ) p π ( s 2 ∣ s 3 ) p π ( s 3 ∣ s 3 ) p π ( s 4 ∣ s 3 ) p π ( s 1 ∣ s 4 ) p π ( s 2 ∣ s 4 ) p π ( s 3 ∣ s 4 ) p π ( s 4 ∣ s 4 ) ] ⏟ P π [ v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) ] ⏟ v π . \underbrace{ \begin{bmatrix} v_{\pi}(s_1)\\ v_{\pi}(s_2)\\ v_{\pi}(s_3)\\ v_{\pi}(s_4) \end{bmatrix}}_{\mathbf{v}_{\pi}} = \underbrace{ \begin{bmatrix} r_{\pi}(s_1)\\ r_{\pi}(s_2)\\ r_{\pi}(s_3)\\ r_{\pi}(s_4) \end{bmatrix}}_{\mathbf{r}_{\pi}} +\gamma\, \underbrace{ \begin{bmatrix} p_{\pi}(s_1\mid s_1) & p_{\pi}(s_2\mid s_1) & p_{\pi}(s_3\mid s_1) & p_{\pi}(s_4\mid s_1)\\ p_{\pi}(s_1\mid s_2) & p_{\pi}(s_2\mid s_2) & p_{\pi}(s_3\mid s_2) & p_{\pi}(s_4\mid s_2)\\ p_{\pi}(s_1\mid s_3) & p_{\pi}(s_2\mid s_3) & p_{\pi}(s_3\mid s_3) & p_{\pi}(s_4\mid s_3)\\ p_{\pi}(s_1\mid s_4) & p_{\pi}(s_2\mid s_4) & p_{\pi}(s_3\mid s_4) & p_{\pi}(s_4\mid s_4) \end{bmatrix}}_{\mathbf{P}_{\pi}} \underbrace{ \begin{bmatrix} v_{\pi}(s_1)\\ v_{\pi}(s_2)\\ v_{\pi}(s_3)\\ v_{\pi}(s_4) \end{bmatrix}}_{\mathbf{v}_{\pi}}. v π v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) = r π r π ( s 1 ) r π ( s 2 ) r π ( s 3 ) r π ( s 4 ) + γ P π p π ( s 1 ∣ s 1 ) p π ( s 1 ∣ s 2 ) p π ( s 1 ∣ s 3 ) p π ( s 1 ∣ s 4 ) p π ( s 2 ∣ s 1 ) p π ( s 2 ∣ s 2 ) p π ( s 2 ∣ s 3 ) p π ( s 2 ∣ s 4 ) p π ( s 3 ∣ s 1 ) p π ( s 3 ∣ s 2 ) p π ( s 3 ∣ s 3 ) p π ( s 3 ∣ s 4 ) p π ( s 4 ∣ s 1 ) p π ( s 4 ∣ s 2 ) p π ( s 4 ∣ s 3 ) p π ( s 4 ∣ s 4 ) v π v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) .
[ v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) ] = [ 0.5 ( 0 ) + 0.5 ( − 1 ) 1 1 1 ] + γ [ 0 0.5 0.5 0 0 0 0 1 0 0 0 1 0 0 0 1 ] [ v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) ] . \begin{bmatrix} v_{\pi}(s_1)\\ v_{\pi}(s_2)\\ v_{\pi}(s_3)\\ v_{\pi}(s_4) \end{bmatrix} = \begin{bmatrix} 0.5(0)+0.5(-1)\\ 1\\ 1\\ 1 \end{bmatrix} +\gamma \begin{bmatrix} 0 & 0.5 & 0.5 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} v_{\pi}(s_1)\\ v_{\pi}(s_2)\\ v_{\pi}(s_3)\\ v_{\pi}(s_4) \end{bmatrix}. v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) = 0.5 ( 0 ) + 0.5 ( − 1 ) 1 1 1 + γ 0 0 0 0 0.5 0 0 0 0.5 0 0 0 0 1 1 1 v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) .
v π = r π + γ P π v π \mathbf{v}_{\pi}=\mathbf{r}_{\pi}+\gamma \mathbf{P}_{\pi}\mathbf{v}_{\pi} v π = r π + γ P π v π
q π ( s , a ) = E [ G t ∣ S t = s , A t = a ] q_{\pi}(s,a) = \mathbb{E}\left[ G_t \mid S_t = s, A_t = a \right] q π ( s , a ) = E [ G t ∣ S t = s , A t = a ]
根据条件期望的性质可得:
E [ G t ∣ S t = s ] ⏟ v π ( s ) = ∑ a E [ G t ∣ S t = s , A t = a ] ⏟ q π ( s , a ) π ( a ∣ s ) \underbrace{\mathbb{E}\left[ G_t \mid S_t = s \right]}_{v_{\pi}(s)} = \sum_{a} \underbrace{\mathbb{E}\left[ G_t \mid S_t = s, A_t = a \right]}_{q_{\pi}(s,a)} \pi(a \mid s) v π ( s ) E [ G t ∣ S t = s ] = a ∑ q π ( s , a ) E [ G t ∣ S t = s , A t = a ] π ( a ∣ s )
因此,
v π ( s ) = ∑ a π ( a ∣ s ) q π ( s , a ) v_{\pi}(s) = \sum_{a} \pi(a \mid s) q_{\pi}(s,a) v π ( s ) = a ∑ π ( a ∣ s ) q π ( s , a )
比较状态价值公式,得到动作价值公式
q π ( s , a ) = ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) q_{\pi}(s,a) = \sum_{r} p(r \mid s,a) r + \gamma \sum_{s'} p(s' \mid s,a) v_{\pi}(s') q π ( s , a ) = r ∑ p ( r ∣ s , a ) r + γ s ′ ∑ p ( s ′ ∣ s , a ) v π ( s ′ )
注意:
动作价值很重要,可以决定选择哪个动作 可以通过状态价值而计算动作价值 也可以直接计算动作价值,通过数据,可以依赖模型或不依赖模型