由表格转为函数,由离散转为连续。用函数拟合连续的状态价值
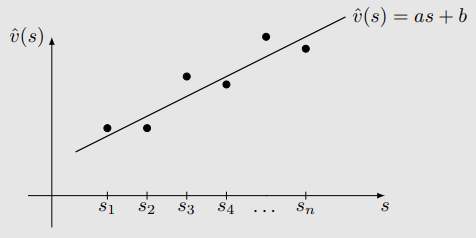
v^(s)=as+b
假设直线的方程为:
v^(s,w)=as+b=[s1][ab]=ϕT(s)w
其中:
- w 是参数向量
- ϕ(s) 是状态 s 的特征向量
- v^(s,w) 关于 w 是线性的
差异 1:如何获取状态值
- 当状态值是用表格表示时,我们可以直接从表中读取值;
- 当状态值是用函数表示时,我们需要将状态索引 s 输入函数,并计算其函数值:
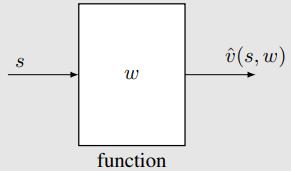
例如: s→ϕ(s)→ϕT(s)w=v^(s,w)
- **优势:存储节省。**我们不需要存储 ∣S∣ 个状态值,只需存储低维参数向量 w。
差异 2:如何更新状态值
- 当状态值是用表格表示时,我们可以直接修改表中对应值;
- 当状态值是用函数表示时,我们必须间接地通过更新 w 来改变值。
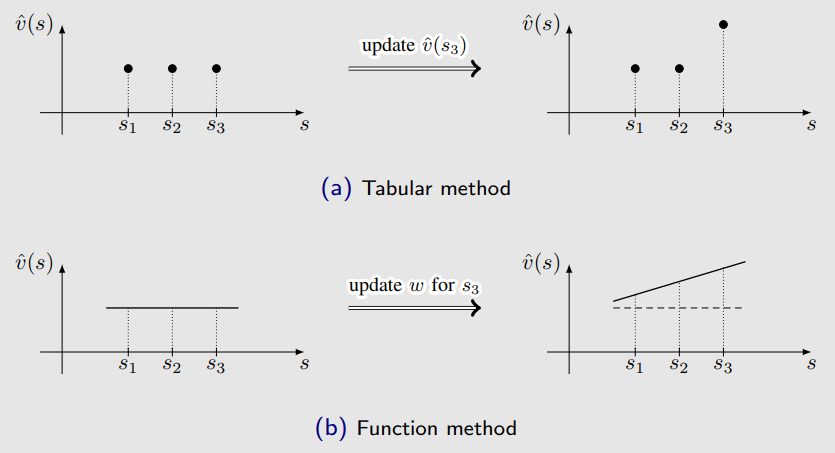
优势:泛化能力(generalization ability)
当我们通过更新 w 来改变 v^(s,w) 时,相邻状态的值也会被相应更新。
函数逼近的好处不是免费的,它也带来了代价:状态值无法被完全准确表示。
因此,这种方法被称为逼近(approximation)。
我们可以使用更高阶的曲线拟合点:
v^(s,w)=as2+bs+c=[s2s1]abc=ϕT(s)w
在这种情况下:
w 和 ϕ(s) 的维度将增加,拟合可能会更加精确;
尽管 v^(s,w) 关于 s 是非线性的,但它仍然是关于 w 的线性函数。
非线性被封装在 ϕ(s) 中。
核心思想:
使用参数化函数来逼近状态值和动作值:v^(s,w)≈vπ(s),其中 w∈Rm 是参数向量。
关键区别:
如何获取和修改 v(s) 的值。
优点:
- 存储效率: w 的维度可能远小于 ∣S∣
- 泛化能力: 一旦状态 s 被访问,参数 w 被更新,其他未访问状态的值也可能被间接更新。
以更正式的方式引入:
- 设 vπ(s) 和 v^(s,w) 分别为真实状态价值与估计状态价值。
- 我们的目标是找到一个最优的参数 w,使得 v^(s,w) 能尽可能逼近 vπ(s),对所有状态 s 成立。
- 这是一个策略评估问题(policy evaluation problem)。
为了找到最优的 w,我们需要 两个步骤:
- 第一步是定义目标函数(objective function)。
- 第二步是推导优化该目标函数的算法。
目标函数(Objective Function) 定义为:
J(w)=E[(vπ(S)−v^(S,w))2]
- 我们的目标是找到最优的 w,使得 J(w) 最小。
- 这个期望是对随机变量 S∈S 的分布而言的。
- 这是新的内容。我们此前还没有讨论过状态的概率分布。
- 实际上,有多种方式可以定义状态 S 的概率分布。
方法一:使用均匀分布(uniform distribution)
- 即认为所有状态同等重要,将每个状态的概率设置为 1/∣S∣。
- 此时目标函数为:
J(w)=E[(vπ(S)−v^(S,w))2]=∣S∣1s∈S∑(vπ(s)−v^(s,w))2
- 缺点:
- 状态可能并不等重要。例如某些状态在策略下几乎不会被访问,这种方式无法体现马尔可夫过程中的真实动态。
方法二:使用平稳分布(stationary distribution)
- 平稳分布是本课程中将频繁使用的重要概念,描述的是马尔可夫过程的长期行为(long-run behavior)。
- 设 {dπ(s)}s∈S 为策略 π 下马尔可夫过程的平稳分布,满足:
dπ(s)≥0,s∈S∑dπ(s)=1
J(w)=E[(vπ(S)−v^(S,w))2]=s∈S∑dπ(s)(vπ(s)−v^(s,w))2
更多说明:
- Distribution:指状态的分布;
- Stationary:表示长期行为;
- 总结:当智能体在策略下运行足够长时间后,任意时刻其处于某状态的概率由该分布描述。
相关信息
- 平稳分布也称为稳态分布(steady-state distribution)或极限分布(limiting distribution)
- 它是理解**值函数方法(value function method)**的关键;
- 它对下一讲中的**策略梯度方法(policy gradient method)**也非常重要。
平稳分布的估计方法示例
- 给定一策略(图中已示意);
- 设 nπ(s) 表示状态 s 在策略 π 下生成的一个很长 episode 中被访问的次数;
- 那么 dπ(s) 可近似为:
dπ(s)≈∑s′∈Snπ(s′)nπ(s)
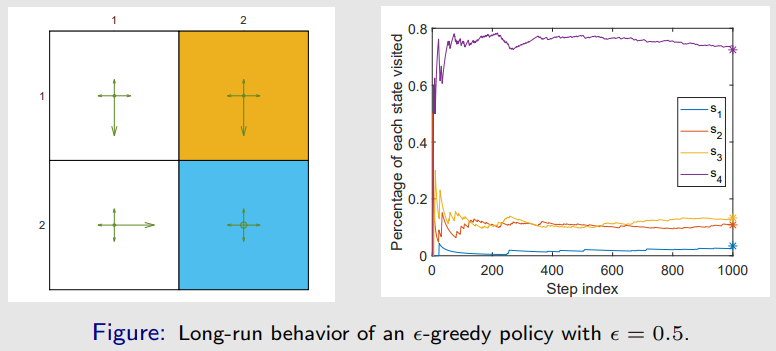
平稳分布的精确解法(通过转移矩阵)
- 收敛的状态概率可以预测,因为它们是平稳分布 dπ 的组成部分:
dπT=dπTPπ
Pπ=0.30.10.100.10.300.10.600.30.100.60.60.8
dπ=[0.0345,0.1084,0.1330,0.7241]T
当我们得到了目标函数后,下一步就是优化它。
- 为了最小化目标函数 J(w),我们可以使用梯度下降法(gradient descent):
wk+1=wk−αk∇wJ(wk)
真实梯度为:
∇wJ(w)=∇wE[(vπ(S)−v^(S,w))2]=E[∇w(vπ(S)−v^(S,w))2]=2E[(vπ(S)−v^(S,w))(−∇wv^(S,w))]=−2E[(vπ(S)−v^(S,w))∇wv^(S,w)]
我们可以用**随机梯度(stochastic gradient)**来代替真实梯度:
wk+1=wk+αkE[(vπ(S)−v^(S,w))∇wv^(S,w)]⇓(用采样近似期望)wt+1=wt+αt(vπ(st)−v^(st,wt))∇wv^(st,wt)
其中 st 是从 S 中采样得到的状态,2αt 被吸收进了新的学习率 αt。
- 理论上,采样应满足平稳分布。但实际中未必成立;
- 该算法不可实现(not implementable),因为它需要真实值 vπ(st),而这正是我们要估计的;
- 可以用对 vπ(st) 的估计值来替代,从而使算法可实现。
两种可实现的近似方法
1. Monte Carlo 函数逼近方法
令 gt 为从 st 开始的折扣回报,则可以用 gt 来近似 vπ(st)。算法更新为:
wt+1=wt+αt(gt−v^(st,wt))∇wv^(st,wt)
2. TD 学习函数逼近方法
根据 TD 学习的思想,用 TD目标 作为 vπ(st) 的近似:
rt+1+γv^(st+1,wt)
于是算法变为:
wt+1=wt+αt[rt+1+γv^(st+1,wt)−v^(st,wt)]∇wv^(st,wt)
TD 学习 + 函数逼近

相关信息
该算法只能估计给定策略下的状态价值函数。理解它对于之后学习其他更复杂的算法是非常重要的。
第一种方法,也就是以前广泛使用的方法,是使用一个线性函数:
v^(s,w)=ϕT(s)w
其中,ϕ(s) 是特征向量,可以是多项式基函数、傅里叶基函数等。
第二种方法,也就是现在广泛使用的方法,是使用神经网络作为非线性函数逼近器。
- 例如,输入是 s,输出是 v^(s,w),参数是 w。
在线性情况下,v^(s,w)=ϕT(s)w,我们有:
∇wv^(s,w)=ϕ(s)
将该梯度代入TD算法:
wt+1=wt+αt[rt+1+γv^(st+1,wt)−v^(st,wt)]∇wv^(st,wt)
得:
wt+1=wt+αt[rt+1+γϕT(st+1)wt−ϕT(st)wt]ϕ(st)
这是使用线性函数逼近的TD学习算法。在本文中,这个算法被称为 TD-Linear。
线性函数方法的缺点:
线性函数方法的优点:
- TD算法在线性情形下的理论性质比非线性情形更容易理解。
- 线性函数逼近仍然非常有用,因为表格表示(tabular representation)是线性函数表示的一种特殊情况。
考虑状态 s 的一个特殊特征向量:
ϕ(s)=es∈R∣S∣
其中 es 是一个向量,其第 s 项为1,其它为0。
在这种情况下:
v^(s,w)=ϕT(s)w=esTw=w(s)
其中 w(s) 是向量 w 的第 s 项。
回顾 TD-Linear 算法:
wt+1=wt+αt[rt+1+γϕT(st+1)wt−ϕT(st)wt]ϕ(st)
当 ϕ(st)=est,上述算法变为:
wt+1=wt+αt(rt+1+γwt(st+1)−wt(st))est
这是一个向量更新公式,仅更新 wt 的第 st 项。
在等式两边同时乘以 estT 得:
wt+1(st)=wt(st)+αt(rt+1+γwt(st+1)−wt(st))
这正是表格形式的 TD 算法(此处称为 TD-Table)。
总结:TD-Linear 在选择了特殊特征向量的情况下变成 TD-Table。
略
该算法:
wt+1=wt+αt[rt+1+γv^(st+1,wt)−v^(st,wt)]∇wv^(st,wt)
并不会最小化以下目标函数:
J(w)=E[(vπ(S)−v^(S,w))2]
不同的目标函数(Objective Functions):
目标函数 1:真实值误差(True value error)
JE(w)=E[(vπ(S)−v^(S,w))2]=∥v^(w)−vπ∥D2
目标函数 2:Bellman误差
JBE(w)=∥v^(w)−(rπ+γPπv^(w))∥D2=∥v^(w)−Tπ(v^(w))∥D2
其中,Tπ(⋅)是贝尔曼算子:
Tπ(x)≐rπ+γPπx
目标函数 3:投影 Bellman 误差(Projected Bellman error)
JPBE(w)=∥v^(w)−MTπ(v^(w))∥D2
其中 M 是一个正交投影矩阵,它在几何上将任意向量投影到函数能够近似的值空间上。
- TD-Linear 算法最小化的是投影 Bellman 误差。
到目前为止,我们只是考虑了状态值估计(state value estimation),即:
v^(s)≈vπ(s),s∈S
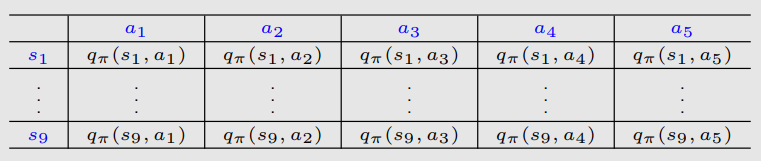
但为了搜索最优策略,我们需要估计的是动作值(action values)。
使用值函数逼近的 Sarsa 算法(SARSA with function approximation)如下:
wt+1=wt+αt[rt+1+γq^(st+1,at+1,wt)−q^(st,at,wt)]∇wq^(st,at,wt)
这和之前我们介绍的算法几乎一样,唯一的区别是将 v^ 替换成了 q^(状态估计值)。
为了搜索最优策略,我们可以结合 策略评估(policy evaluation) 和 策略改进(policy improvement)。

总结:这是一个典型的基于值函数的策略迭代过程,在每一步:
- 利用当前策略采样轨迹(policy evaluation)
- 用 q 值更新策略(policy improvement)
与 Sarsa 类似,表格型 Q-learning 也可以扩展到 值函数逼近 的情形。
Q 值的更新规则如下:
wt+1=wt+αt[rt+1+γa∈A(st+1)maxq^(st+1,a,wt)−q^(st,at,wt)]∇wq^(st,at,wt)
这和 Sarsa 算法 几乎一样,唯一的区别在于:
q^(st+1,at+1,wt)被替换为a∈A(st+1)maxq^(st+1,a,wt)
中文解释:
- Sarsa 是on-policy(同策略)方法,用的是实际采取的 at+1
- Q-learning 是off-policy(异策略)方法,用的是当前估计下最优动作对应的 Q 值,即对 a 取最大值
- 两者都使用近似函数 q^(s,a,w) 来估计 Q 值,参数更新公式的结构相同,区别只在于目标值(target)
Q-learning with function approximation (on-policy version)

是最早期且最成功的将深度神经网络引入强化学习的算法之一。
神经网络的作用是作为一个非线性函数逼近器。
它与以下算法不同:
wt+1=wt+αt[rt+1+γa∈A(st+1)maxq^(st+1,a,wt)−q^(st,at,wt)]∇wq^(st,at,wt)
不同之处在于训练神经网络的方式。
目标是最小化如下目标函数/损失函数:
wt+1=wt+αt[rt+1+γa∈A(st+1)maxq^(st+1,a,wt)−q^(st,at,wt)]∇wq^(st,at,wt)⇓J(w)=E[(R+γa∈A(S′)maxq^(S′,a,w)−q^(S,A,w))2]
其中 (S,A,R,S′) 是随机变量。
如何计算目标函数的梯度?——很棘手!
这是因为,在该目标函数中:
J(w)=E[(R+γa∈A(S′)maxq^(S′,a,w)−q^(S,A,w))2]
参数 w 不仅出现在 q^(S,A,w) 中,还出现在:
y≐R+γa∈A(S′)maxq^(S′,a,w)
由于最优动作 a 依赖于 w,
∇wy=γa∈A(S′)max∇wq^(S′,a,w)
为了解决这个问题,我们可以假设在计算梯度时,y 中的 w 是固定的(至少在一段时间内)。
为此,我们可以引入两个网络。
- 一个是主网络(main network),表示 q^(s,a,w)
- 另一个是目标网络(target network),q^(s,a,wT)
在这种情况下,目标函数简化为:
J=E[(R+γa∈A(S′)maxq^(S′,a,wT)−q^(S,A,w))2]
其中 wT 是目标网络的参数。
当 wT 被固定时,J 的梯度可以简单计算为:
∇wJ=E[(R+γa∈A(S′)maxq^(S′,a,wT)−q^(S,A,w))∇wq^(S,A,w)]
- Deep Q-learning 的基本思想是使用梯度下降算法来最小化该目标函数。
- 然而,这样的优化过程涉及一些重要的技巧,值得特别关注。
实现细节:
令 w 和 wT 分别表示主网络与目标网络的参数。它们最初被设置为相同。
在每一次迭代中,我们从 replay buffer(回放缓冲区,见下文) 中抽取一个 mini-batch 样本 {(s,a,r,s′)}。
对于每个 (s,a,r,s′),我们可以计算期望的输出:
yT≐r+γa∈A(s′)maxq^(s′,a,wT)
因此,我们得到一个 mini-batch 数据:
{(s,a,yT)}
使用 {(s,a,yT)} 来训练网络,从而最小化:
(yT−q^(s,a,w))2
当我们收集了一些经验样本之后,我们不会按它们被收集的顺序使用它们。
相反,我们将它们存储在一个集合中,称为 replay buffer:
B≐{(s,a,r,s′)}
每次训练神经网络时,我们可以从 replay buffer 中随机抽取一个 mini-batch 样本。
抽样过程(也叫经验回放 experience replay)应遵循均匀分布(uniform distribution)。
问题:为什么经验回放在 deep Q-learning 中是必要的?为什么 replay 必须服从均匀分布?
解答:
答案可以从目标函数中看出:
J=E[(R+γa∈A(S′)maxq^(S′,a,w)−q^(S,A,w))2]
R∼p(R∣S,A),S′∼p(S′∣S,A):R 和 S 是由系统模型决定的。
(S,A)∼d:(S,A) 是一个索引,被看作一个单独的随机变量。
状态-动作对 (S,A) 的分布被假设为均匀的。
- 为什么要均匀分布?因为我们没有先验知识(no prior knowledge)。
- 我们能像之前那样使用平稳分布吗?不能,因为没有给定策略。
然而,样本并不是均匀采样的,因为它们是由某个策略连续生成的。
为了打破连续样本之间的相关性,我们可以使用经验回放技术,从 replay buffer 中均匀地采样。
这就是数学上的原因,说明了为什么经验回放是必要的,为什么它必须是均匀的。
回顾表格形式的 Q-learning:
**问题:**为什么表格 Q-learning 不需要经验回放?
- **回答:**因为它不需要对 S 或 A 进行分布建模。
**问题:**为什么 Deep Q-learning 涉及分布问题?
**回答:**因为我们需要定义一个标量目标函数:
J(w)=E[∗]
其中期望是对所有 (S,A) 取的。
表格形式旨在解一组关于所有 (s,a) 的方程(Bellman 最优性方程),而 deep Q-learning 是优化一个标量目标函数。
**问题:**我们能在表格 Q-learning 中使用经验回放吗?
- **回答:**是的,我们可以,而且可以提高样本效率。
总结:
- 表格法不用经验回放,是因为它没有“泛化”和“梯度不稳定”的问题;
- DQN 必须用经验回放,是因为神经网络对数据分布、相关性、非平稳性极其敏感。
Deep Q-learning (off-policy version)

Remarks:
- 策略由最终的动作值决定(贪婪),不需要策略更新。
- 该网络的输入输出和原始论文不一致
- 这个伪代码用的是:(s,a)→Q(s,a)
- 而原论文用的是:s→[Q(s,a1),...,Q(s,an)]
- 我们需要为每一个状态-动作对学习最优动作价值(learn optimal action values for every state-action pair)。
- 一旦获得最优动作价值,最优的贪婪策略(greedy policy)可以立即获得。
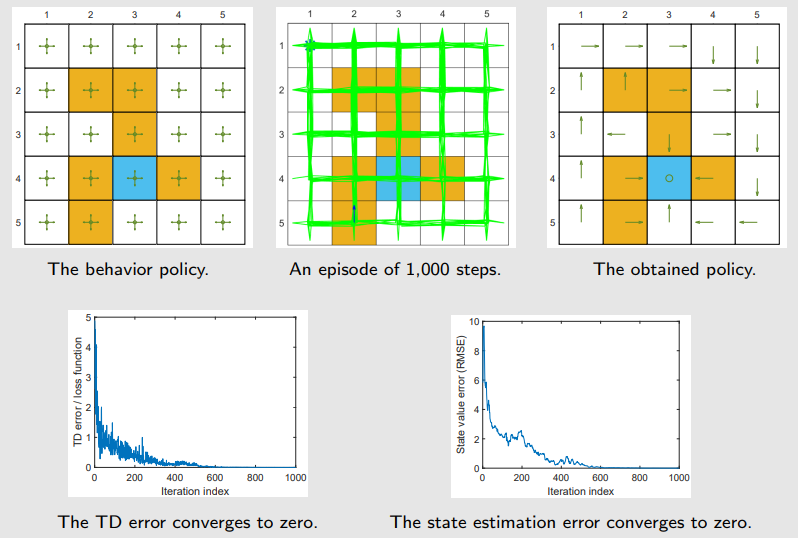
Setup:
- 使用单个 episode 来训练神经网络。
- 该 episode 是通过图(a)中展示的一个**探索性行为策略(exploratory behavior policy)**生成的。
- 该 episode 仅有 1000 步!(而表格型 Q-learning 需要 100,000 步)。
- 一个具有单个隐藏层的浅层神经网络被用作 q^(s,a,w) 的非线性逼近器。
- 该隐藏层包含 100 个神经元(neurons)。