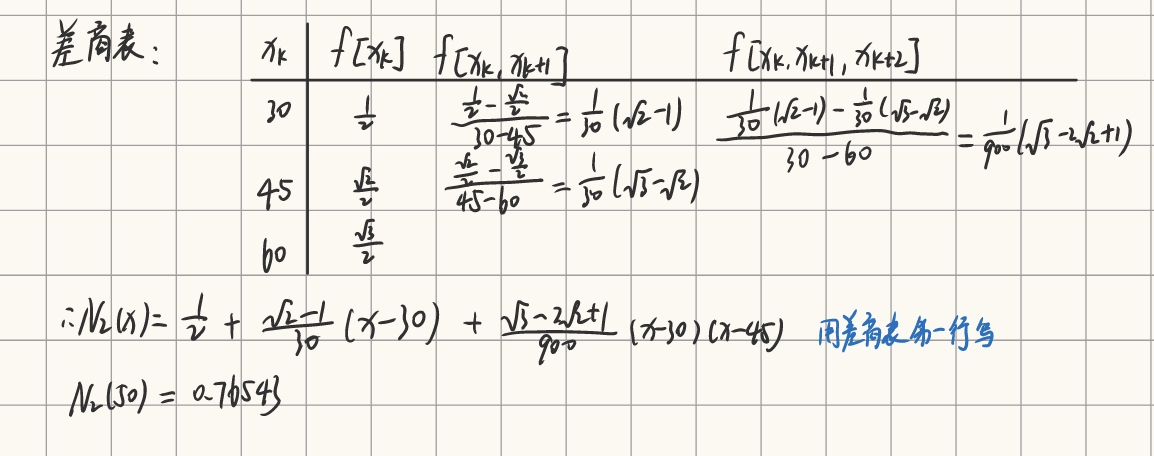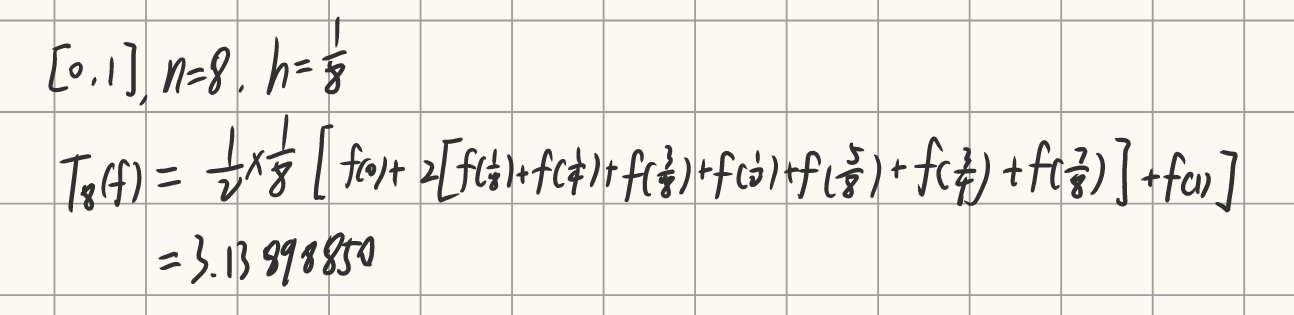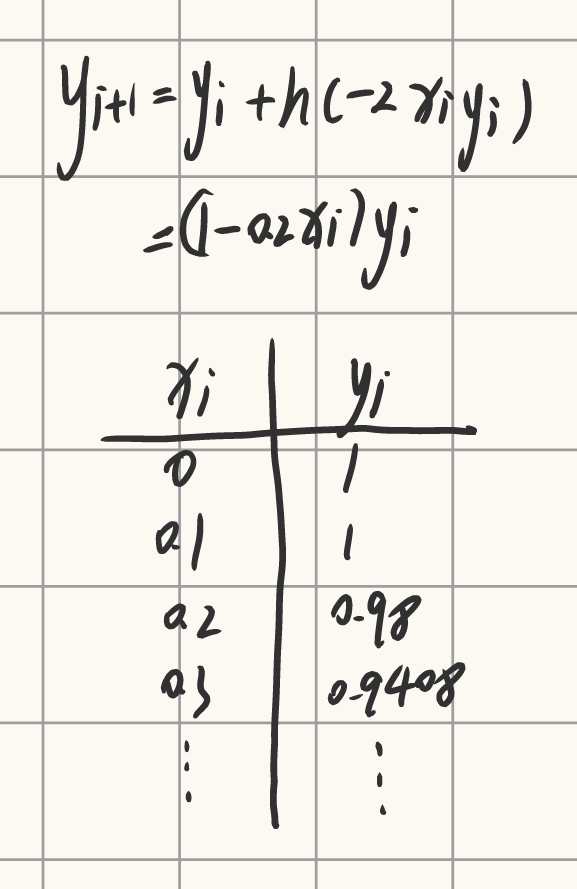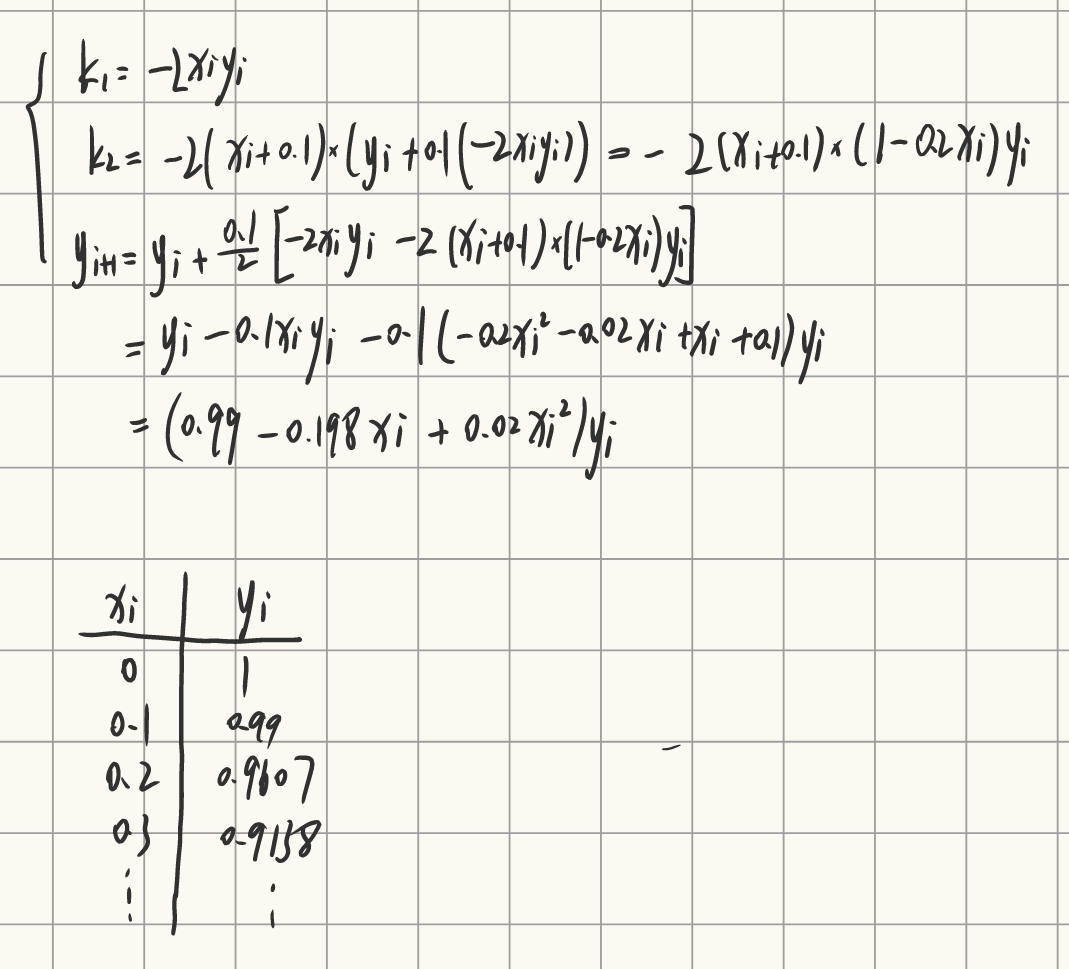计算方法必考题

1. 误差的分类

填空题

误差的分类

2. 求近似值的有效数字位数

定义: 若 $| x-x^* | \leq 0.5 \times 10^{-k}$ , 则 x 从左起第一个非零数字到第 k 位数字均为有效数字，共 k 位。

判定规则：

1. 非零开头数：从左起第一个非零数字开始，到最末一位数字为止，所有数字均为有效数字
2. 科学计数法表示的数：形如 $a \times 10^n$ 时，有效数字由数字 a 决定
3. 整数末尾的零：需说明精度
   • 如果末尾零是有效数字
   • 如果仅为定位作用，不算有效数字
4. 运算结果的有效数字：
   • 加法与减法：结果应保留到小数点后最少位数的那个数的小数位数。例如，$3.14 + 2.5 = 5.6$（因为 $2.5$ 只有一位小数）。
   • 乘法与除法：结果应保留与参与运算中有效数字最少的数相同的有效数字位数。例如，$1.23 \times 0.0045 = 0.0055$（因为 $0.0045$ 有 2 位有效数字，结果也应保留 2 位有效数字）。

填空题

求近似值有效位数

3. 秦九韶法求多项式的值

计算题

求 $f(x)=2+x-x^2+3x^4$ 在点 $x_0=2$ 处的值

4. LU分解法求方程的解

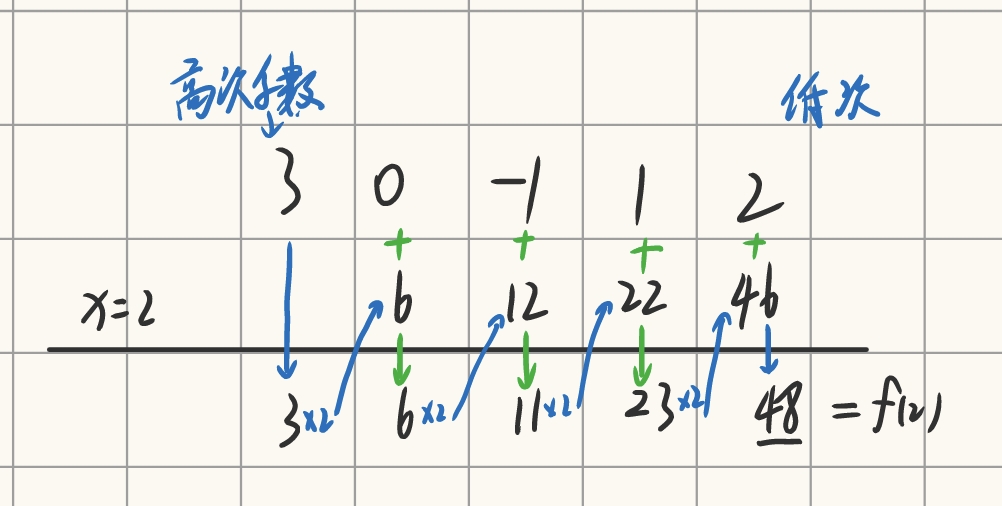
计算题

$$\begin{bmatrix} 2 & 2 & -1 \\ 1 & -1 & 0 \\ 4 & -2 & -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} -4 \\ 0 \\ -6 \end{bmatrix}$$

5. 向量范数与矩阵范数

类型	向量 $1$ 范数 $|\mathbf{x}|_1$	向量 $\infty$ 范数 $|\mathbf{x}|_\infty$	矩阵 $1$ 范数 $|\mathbf{A}|_1$	矩阵 $\infty$ 范数 $|\mathbf{A}|_\infty$
公式	$\sum\limits_{i=1}^{n}|x_i|$	$\max\limits_i |x_i|$	$\max\limits_j \sum\limits_i |a_{ij}|$	$\max\limits_i \sum\limits_j |a_{ij}|$
本质	元素绝对值之和	最大元素绝对值	最大列元素绝对值之和	最大行元素绝对值之和
示例	$\lVert[2,-3,0,5]\rVert_1 = 10$	$\lVert[2,-3,0,5]\rVert_{\infty} = 5$	$\left\lVert\begin{bmatrix}1 & -2 \\ 3 & 4 \\ -1 & 0\end{bmatrix}\right\rVert_1 = 6$	$\left\lVert\begin{bmatrix}1 & -2 \\ 3 & 4 \\ -1 & 0\end{bmatrix}\right\rVert_{\infty} = 7$

类型	公式	本质	计算示例（以向量 $\mathbf{x} = [2, -3, 5]$ 和矩阵 $A = \begin{bmatrix}1&-2\\3&4\end{bmatrix}$ 为例）
向量二范数	$\lVert \mathbf{x} \rVert_2 = \sqrt{\sum_{i=1}^{n} |x_i|^2}$	欧氏空间中向量的长度（模长）	$\lVert \mathbf{x} \rVert_2 = \sqrt{2^2 + (-3)^2 + 5^2} = \sqrt{38} \approx 6.16$
矩阵二范数（谱范数）	$\lVert A \rVert_2 = \sqrt{\lambda_{\text{max}}(A^T A)}$	矩阵 $A^T A$ 的最大特征值的平方根，反映矩阵对向量的最大“拉伸”能力	1. 计算 $A^T A = \begin{bmatrix}1&3\\-2&4\end{bmatrix}\begin{bmatrix}1&-2\\3&4\end{bmatrix} = \begin{bmatrix}10&10\\10&20\end{bmatrix}$ 2. 求特征值：$\lambda_1 = 30, \lambda_2 = 0$ 3. $\lVert A \rVert_2 = \sqrt{30} \approx 5.48$

填空题

向量范数和矩阵范数的一范数和无穷范数

6. 雅可比迭代法与高斯-赛德尔迭代法

迭代矩阵

设线性方程组为 $Ax = b$，其中 $A \in \mathbb{R}^{n \times n}$ 为非奇异矩阵。将 $A$ 分解为：

• $D = \mathrm{diag}(a_{11}, a_{22}, \dots, a_{nn})$，对角元素构成的对角矩阵；
• $L$ 为严格下三角矩阵（主对角线元素为 $0$）；
• $U$ 为严格上三角矩阵（主对角线元素为 $0$）；满足：$A = D + L + U$

雅可比迭代矩阵 :

$$J=-D^{-1}(L+U)$$

雅可比迭代格式：

$$x^{(k+1)} = Jx^{(k)}+D^{-1}b$$

高斯-赛德尔迭代矩阵 ：

$$G=-(D+L)^{-1}U$$

高斯赛德尔迭代公式：

$$x^{(k+1)} = Gx^{(k)}+(D+L)^{-1}b$$

填空题

雅可比迭代法和高斯-赛德尔迭代法的迭代矩阵

7. 拉格朗日插值多项式

公式

拉格朗日插值基函数：

$$l_i(x) = \prod\limits_{\substack{j=0 \\ j \ne i}}^{n} \frac{x - x_j}{x_i - x_j}$$

n次拉格朗日插值多项式（n+1个点）：

$$L_n(x) = \sum\limits_{i=0}^{n} f(x_i) \cdot l_i(x)$$

二次 3个点

$$L_2(x) = f(x_0)l_0(x) + f(x_1)l_1(x) + f(x_2)l_2(x) \\ l_0(x) = \frac{(x - x_1)(x - x_2)}{(x_0 - x_1)(x_0 - x_2)} \\ l_1(x) = \frac{(x - x_0)(x - x_2)}{(x_1 - x_0)(x_1 - x_2)} \\ l_2(x) = \frac{(x - x_0)(x - x_1)}{(x_2 - x_0)(x_2 - x_1)}$$

三次 4个点

$$L_3(x) = f(x_0)l_0(x) + f(x_1)l_1(x) + f(x_2)l_2(x) + f(x_3)l_3(x) \\ l_0(x) = \frac{(x - x_1)(x - x_2)(x - x_3)}{(x_0 - x_1)(x_0 - x_2)(x_0 - x_3)} \\ l_1(x) = \frac{(x - x_0)(x - x_2)(x - x_3)}{(x_1 - x_0)(x_1 - x_2)(x_1 - x_3)} \\ l_2(x) = \frac{(x - x_0)(x - x_1)(x - x_3)}{(x_2 - x_0)(x_2 - x_1)(x_2 - x_3)} \\ l_3(x) = \frac{(x - x_0)(x - x_1)(x - x_2)}{(x_3 - x_0)(x_3 - x_1)(x_3 - x_2)}$$

插值余项（误差估计）

n+1阶导数存在时：

$$R_n(x) = f(x) - L_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!} \cdot \prod_{i=0}^{n}(x - x_i)$$

计算题

已知 $f(x)=\sin x, x\in[0,\pi]$。
(1)以 $x_0 = 0, x_1=\frac{\pi}{2}, x_2 = \pi$ 为插值节点，求 $f(x)$ 的 2 次插值多项式 $L_2(x)$，并作出 $f(x)$ 和 $L_2(x)$ 的图像；
(2)以 $x_0 = 0, x_1=\frac{\pi}{3}, x_2=\frac{2\pi}{3}, x_3 = \pi$ 为插值节点，求 $f(x)$ 的 3 次插值多项式 $L_3(x)$，并作出 $f(x)$ 和 $L_3(x)$ 的图像；
(3)估计插值误差 $|f(x) - L_2(x)|$ 和 $|f(x) - L_3(x)|$ 的上界。

8. 差商及牛顿插值公式

一阶差商：2个点

$$f[x_0, x_1] = \frac{f(x_1) - f(x_0)}{x_1 - x_0}$$

二阶差商：3个点

$$f[x_0, x_1, x_2] = \frac{f[x_1, x_2] - f[x_0, x_1]}{x_2 - x_0}$$

三阶差商：4个点

$$f[x_0, x_1, x_2, x_3] = \frac{f[x_1, x_2, x_3] - f[x_0, x_1, x_2]}{x_3 - x_0}$$

k阶差商：k+1个点

$$f[x_0, x_1, \dots, x_k] = \frac{f[x_1, \dots, x_k] - f[x_0, \dots, x_{k-1}]}{x_k - x_0}$$

差商表：

$$\begin{array}{c|c|c|c|c} x_i & f[x_i] & f[x_i, x_{i+1}] & f[x_i, x_{i+1}, x_{i+2}] & f[x_i, x_{i+1}, x_{i+2}, x_{i+3}] \\ \hline x_0 & f(x_0) & f[x_0,x_1] & f[x_0,x_1,x_2] & f[x_0,x_1,x_2,x_3] \\ x_1 & f(x_1) & f[x_1,x_2] & f[x_1,x_2,x_3] & \\ x_2 & f(x_2) & f[x_2,x_3] & & \\ x_3 & f(x_3) & & & \\ \end{array}$$

填空题

计算差商

牛顿插值多项式：

$$P_n(x) = f[x_0] + f[x_0,x_1](x - x_0) + f[x_0,x_1,x_2](x - x_0)(x - x_1) + \cdots + f[x_0,\dots,x_n](x - x_0)\cdots(x - x_{n-1})$$

计算题

给定数据如下：

$$\begin{array}{c|ccc} x & 30 & 45 & 60 \\ \hline f(x) & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} \\ \end{array}$$

求二次牛顿插值多项式 $N_2(x)$，并求 $N_2(50)$。

9. 最小二乘法曲线拟合

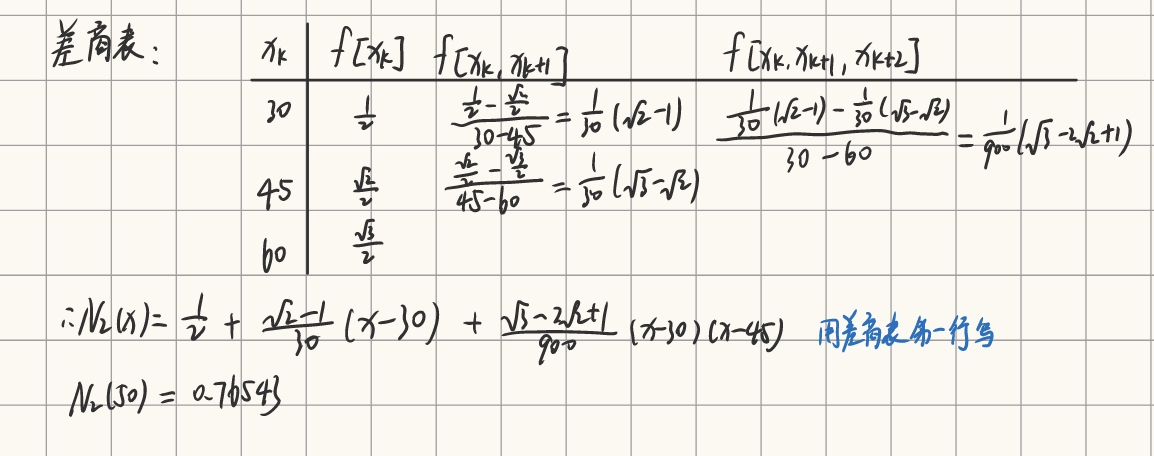
解法：

1. 算正规方程组：

二次多项式

$$\begin{bmatrix} n & \sum x_i & \sum x_i^2 \\ \sum x_i & \sum x_i^2 & \sum x_i^3 \\ \sum x_i^2 & \sum x_i^3 & \sum x_i^4 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix} = \begin{bmatrix} \sum y_i \\ \sum x_i y_i \\ \sum x_i^2 y_i \end{bmatrix}$$

m次多项式

$$\begin{bmatrix} n & \sum x_i & \sum x_i^2 & \cdots & \sum x_i^m \\ \sum x_i & \sum x_i^2 & \sum x_i^3 & \cdots & \sum x_i^{m+1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \sum x_i^m & \sum x_i^{m+1} & \sum x_i^{m+2} & \cdots & \sum x_i^{2m} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_m \end{bmatrix} = \begin{bmatrix} \sum y_i \\ \sum x_i y_i \\ \vdots \\ \sum x_i^m y_i \end{bmatrix}$$

2. 用列主元高斯消去法解正规方程组，其解为曲线系数

计算题

假设实验测得关于变量 $x$ 和 $y$ 的一组数据如表6.2所示，求一个代数多项式曲线（二次），使其最好地拟合这组给定数据。

$i$	1	2	3	4	5	6	7	8	9
$x_i$	1	3	4	5	6	7	8	9	10
$y_i$	10	5	4	2	1	1	2	3	4

计算题

设有如下实验数据：

$x$	1.36	1.49	1.73	1.81	1.95	2.16	2.28	2.48
$y$	14.094	15.096	16.844	17.378	18.435	19.949	20.963	22.494

试用最小二乘法求一个一次多项式拟合以上数据。

略

10. 数值积分

数值积分：核心思想是用插值多项式近似被积函数并积分
代数精度：若求积公式对所有次数≤m 的多项式精确成立，而对 m+1 次多项式不成立，则称其代数精度为 m

插值型

这里n表示多项式次数

梯形公式（n=1，2个节点）：

$$\int_a^b f(x)dx \approx \frac{b-a}{2}[f(a) + f(b)]$$

Simpson(辛普生)公式（n=2，3个节点）：

$$\int_a^b f(x)dx \approx \frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right) + f(b)\right]$$

Simpson 3/8 公式（n=3，4 个节点）：

$$\int_a^b f(x)dx \approx \frac{3(b-a)}{8}\left[f(a) + 3f\left(a+\frac{b-a}{3}\right) + 3f\left(a+\frac{2(b-a)}{3}\right) + f(b)\right]$$

......

一般形式：n阶Cotes公式

$$\int_a^b f(x) \, dx \approx (b-a) \sum_{k=0}^n C_k^{(n)} f(x_k)$$

Cotes 系数表

$n$	$C_0^{(n)}$	$C_1^{(n)}$	$C_2^{(n)}$	$C_3^{(n)}$	$C_4^{(n)}$	$C_5^{(n)}$	$C_6^{(n)}$
1	$\dfrac{1}{2}$	$\dfrac{1}{2}$	-	-	-	-	-
2	$\dfrac{1}{6}$	$\dfrac{4}{6}$	$\dfrac{1}{6}$	-	-	-	-
3	$\dfrac{1}{8}$	$\dfrac{3}{8}$	$\dfrac{3}{8}$	$\dfrac{1}{8}$	-	-	-
4	$\dfrac{7}{90}$	$\dfrac{32}{90}$	$\dfrac{12}{90}$	$\dfrac{32}{90}$	$\dfrac{7}{90}$	-	-
5	$\dfrac{19}{288}$	$\dfrac{75}{288}$	$\dfrac{50}{288}$	$\dfrac{50}{288}$	$\dfrac{75}{288}$	$\dfrac{19}{288}$	-
6	$\dfrac{41}{840}$	$\dfrac{216}{840}$	$\dfrac{27}{840}$	$\dfrac{272}{840}$	$\dfrac{27}{840}$	$\dfrac{216}{840}$	$\dfrac{41}{840}$

高阶系数（n≥7）因可能出现负数且数值不稳定，实际应用较少

复化型

将区间 [a,b] 分成 n 个子区间，每个子区间应用低阶求积公式，提高计算精度

复化梯形公式

$$T_n(f) = \frac{h}{2}\left[f(a) + 2\sum_{k=1}^{n-1}f(a+kh) + f(b)\right] \quad (h=\frac{b-a}{n})$$

计算题

对于 $f(x)=\frac{4}{1 + x^2}$，利用数据表7.1计算积分 $I = \int_{0}^{1}\frac{4}{1 + x^2}\text{d}x$。

$x_k$	0	1/8	1/4	3/8	1/2
$f(x_k)$	4.00000000	3.93846154	3.76470588	3.50684932	3.20000000

$x_k$	5/8	3/4	7/8	1
$f(x_k)$	2.87640449	2.56000000	2.26548673	2.00000000

只考梯形公式

余项

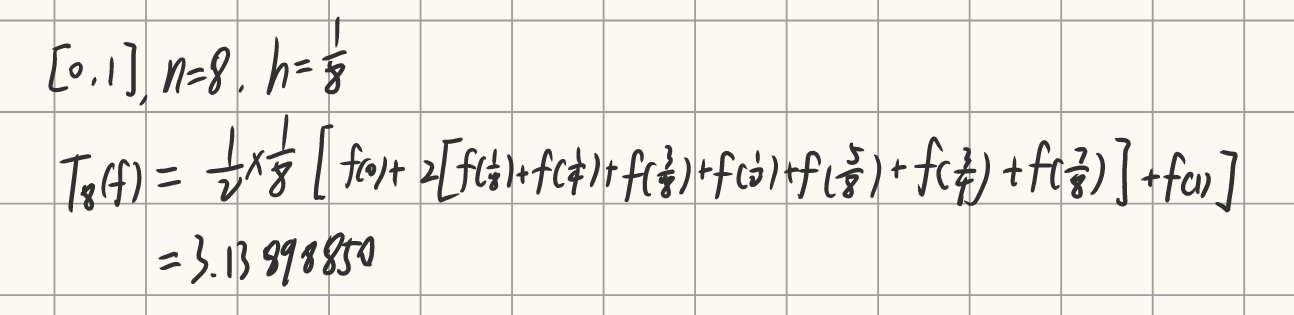
插值型

$$R(f) = \int_a^b f(x) dx - \int_a^b P_n(x) dx = \frac{f^{(n+1)}(\xi)}{(n+1)!} \int_a^b \omega(x) dx, \quad \xi \in (a, b)$$

其中，$\omega(x) = \prod_{i=0}^{n} (x - x_i)$ 是插值节点对应的基函数乘积。

特别的：
梯形公式（$n = 1$）余项：

$$R_T = -\frac{(b - a)^3}{12} f''(\xi), \quad \xi \in (a, b)$$

Simpson公式（$n = 2$）余项：

$$R_S = -\frac{(b - a)^5}{2880} f^{(4)}(\xi), \quad \xi \in (a, b)$$

复化型

复化梯形公式误差：

$$R_T = -\frac{(b - a) h^2}{12} f''(\xi), \quad \xi \in (a, b)$$

复化Simpson公式误差：

$$R_S = -\frac{(b - a) h^4}{180} f^{(4)}(\xi), \quad \xi \in (a, b)$$

代数精度

当取等距节点数为 $n+1$（即公式阶数为 $n$）时：

$$\text{代数精度} = \begin{cases} n+1, & \text{当 } n \text{ 为偶数} \\ n, & \text{当 } n \text{ 为奇数} \end{cases}$$

公式类型	节点数	代数精度	收敛阶数
梯形公式	2	1	2
Simpson公式	3	3	4
Simpson 3/8公式	4	3	4
柯特斯公式	5	5	6
复化梯形公式	n+1	1	2
复化Simpson公式	2n+1	3	4
复化柯特斯公式	4n+1	5	6

表中n表示分成子区间个数

复化求积公式中：

• 收敛阶数 = 代数精度 + 1
• 代数精度同插值型

填空题

各种公式的代数精度

11. 欧拉方法

用差分近似导数，将连续的微分方程转化为离散的递推公式，通过逐步迭代计算出解的近似值。

公式

一阶常微分方程初值问题：

$$\begin{cases} y'(x) = f(x, y) \\ y(x_0) = y_0 \end{cases}$$

导数的差分近似：

$$y'(x_n) \approx \frac{y(x_{n+1}) - y(x_n)}{h}$$

向前欧拉递推公式（单步显式）：

$$y_{n+1} = y_n + h \cdot f(x_n, y_n)$$

向后欧拉递推公式（单步隐式）：

$$y_{n+1} = y_n + h \cdot f(x_{n+1}, y_{n+1})$$

梯形法（单步隐式）：

$$y_{n+1} = y_n + \frac{h}{2} \left[ f(x_n, y_n) + f(x_{n+1}, y_{n+1}) \right]$$

改进欧拉方法：

$$\begin{cases} \text{预测步：} \quad k_1 = f(x_n, y_n) \\ \text{校正步：} \quad k_2 = f(x_n + h, y_n + h \cdot k_1) \\ y_{n+1} = y_n + \frac{h}{2} \cdot (k_1 + k_2) \end{cases}$$

计算题

求解初值问题

$$\begin{cases} y' = -2xy, & 0 \leqslant x \leqslant 1.8, \\ y(0) = 1, \end{cases}$$

取步长 $h = 0.1$。

普通欧拉公式（向前欧拉）

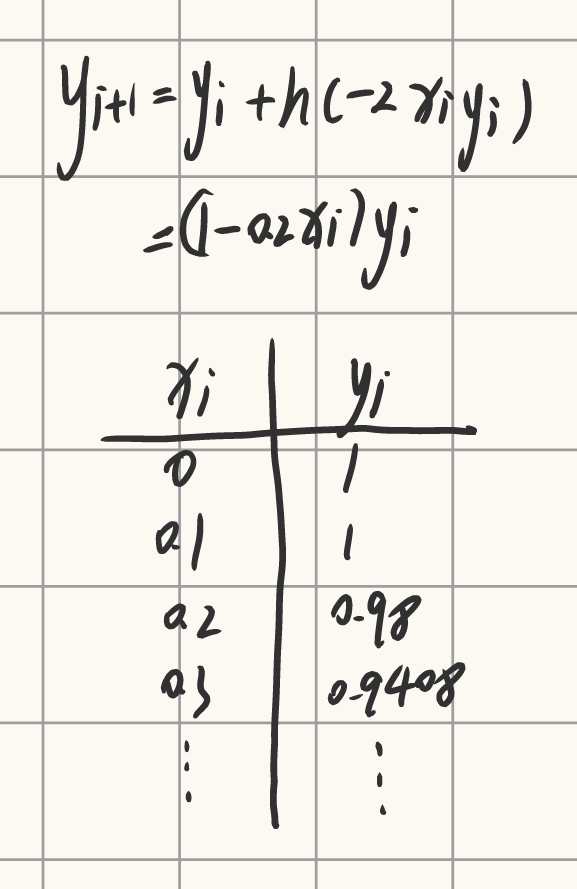
改进欧拉公式

截断误差

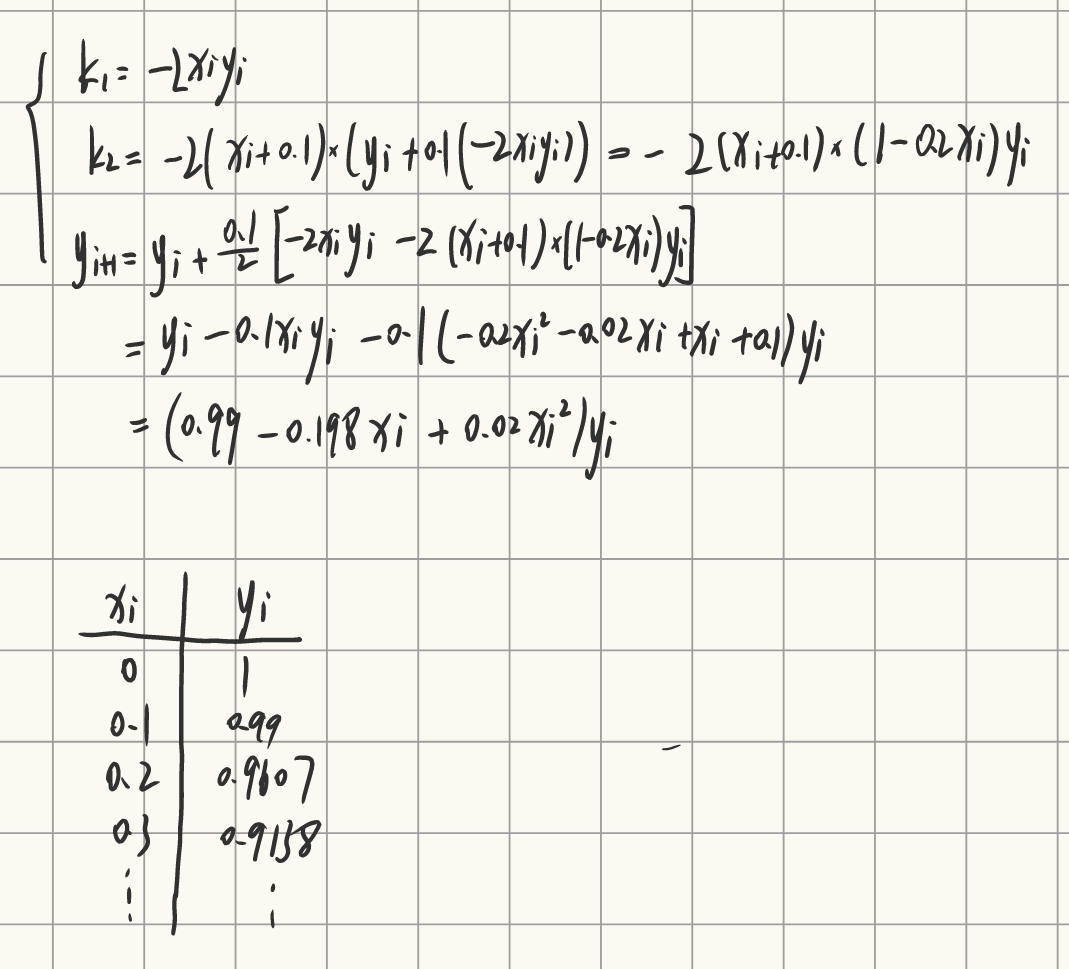
局部截断误差：在单步计算中，假设前一步解精确时，当前步近似解与精确解的偏差

整体截断误差：经过 n 步计算后，近似解与精确解的累积偏差

方法名称	局部截断误差 $T_n$	整体截断误差 $E_n$
前向欧拉法	$T_n = \frac{h^2}{2} y''(\xi_n),\ \xi_n \in (x_n, x_{n+1}),\ \mathcal{O}(h^2)$	$\mathcal{O}(h)$
后向欧拉法	$T_n = \frac{h^2}{2} y''(\xi_n),\ \xi_n \in (x_n, x_{n+1}),\ \mathcal{O}(h^2)$	$\mathcal{O}(h)$
改进欧拉法（Heun法）	$T_n = \frac{h^3}{3} y'''(\xi_n),\ \xi_n \in (x_n, x_{n+1}),\ \mathcal{O}(h^3)$	$\mathcal{O}(h^2)$
梯形法	$T_n = -\frac{h^3}{12} y'''(\xi_n),\ \xi_n \in (x_n, x_{n+1}),\ \mathcal{O}(h^3)$	$\mathcal{O}(h^2)$

填空题

各种方法的局部截断误差